题目内容
6.已知函数f(x)的定义域为实数集R,(1)若函数f(x)=2xsin(πx),证明f(x+2)=4f(x);
(2)若f(x+T)=kf(x)(k>0,T>0),若f(x)=axφ(x)(其中a为正的常数),试证明函数φ(x)是以T为周期的周期函数;
(3)若f(x+6)=$\sqrt{2}$f(x),且当x∈[-3,3]时,f(x)=$\frac{1}{10}$x(x2-9),记Sn=f(2)+f(6)+f(10)+…+f(4n-2)n∈N*,求使得S1、S2、S3…Sn小于1000都成立的最大整数n.
分析 (1)根据条件进行证明即可.
(2)结合条件,进行转化证明.
(3)将f(4n-2)分成三组,分别计算出每组数列的特点,利用等比数列的求和公式进行计算即可.
解答 证明:(1)若f(x)=2xsin(πx),
∴f(x+2)=2x+2sin(πx+2π)=4•2xsin(πx)=4f(x);
(2)若f(x)=axφ(x),
则,满足f(x+T)=kf(x),
即ax+Tφ(x+T)=kaxφ(x),
即aTφ(x+T)=kφ(x),
即φ(x+T)=ka-Tφ(x),
故函数φ(x)是以T为周期的周期函数.
(3)∵若f(x+6)=$\sqrt{2}$f(x),且当x∈[-3,3]时,f(x)=$\frac{1}{10}$x(x2-9),
∴f(2)=-1,f(14)=f(12+2)=($\sqrt{2}$)2f(2)=-2,
则f(2),f(14),f(26)…构成以-1为首项,公比q=2的等比数列,
f(6)=$\sqrt{2}$f(0)=0,
即f(6)=f(18)=f(6k)=…=0,
f(10)=f(12-2)($\sqrt{2}$)2f(-2)=2,
f(22)=f(12+10)=($\sqrt{2}$)2f(10)=2×2=4,
则f(10),f(22),f(34)…构成以2为首项,公比q=2的等比数列,
每相邻三项为一组设n=3k,
则Sn=f(2)+f(6)+f(10)+…+f(4n-2)=$\frac{-1•(1-{2}^{k})}{1-2}$+$\frac{2(1-{2}^{k})}{1-2}$=2k-1+2•2k-2=3•2k-3,
当k=8时,Sn=765,
即当k=8时,n=24,
则当n=25时,f(4n-2)=f(4×25-2)=f(98)=f(16×6+2)=($\sqrt{2}$)16f(2)=-256,
此时S25=765-256=509,
当n=26时,f(4n-2)=f(4×26-2)=f(102)=f(17×6)=0,
此时S26=765-256=509,
当n=27,f(4n-2)=f(4×27-2)=f(106)=f(18×6-2)=($\sqrt{2}$)18f(-2)=512,
此时S27=509+512=1021,
故使得S1、S2、S3…Sn小于1000都成立的最大整数n为26
点评 本题主要考查函数的性质,以及函数与数列的综合,考查学生的运算能力,综合性较强,难度较大.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
| A. | 若a1>0,d>0,则n唯一确定时$s_n^{\;}$也唯一确定 | |
| B. | 若a1>0,d<0,则n唯一确定时$s_n^{\;}$也唯一确定 | |
| C. | 若a1>0,d>0,则$s_n^{\;}$唯一确定时n也唯一确定 | |
| D. | 若a1>0,d<0,则$s_n^{\;}$唯一确定时n也唯一确定 |
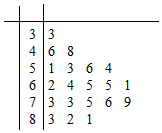 某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意
某公司做了用户对其产品満意度的问卷调查,随机抽取了20名用户的评分,得到图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意(1)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“満意”与“否”与性别有有关?
附:
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(3)从以上男性用户中抽取2人,女性用户中抽取1人,其中满意的人数为ξ,求ξ的分布列与数学期望.
| A. | 90 | B. | 115 | C. | 210 | D. | 385 |
| A. | (-$\frac{1}{3}$,0) | B. | (-$\frac{1}{3}$,1) | C. | (0,2) | D. | (-$\frac{1}{3}$,log32) |