题目内容
1．已知f0（x）=cosxsinx，f1（x）=f0′（x），f2（x）=f1′（x），f3（x）=f2′（x），fn（x）=fn-1′（x），n∈N+，则f2016（x）等于（ ）| A． | sin22015x | B． | 2cosxsinx | C． | -22015cos2x | D． | 22015sin2x |
分析 求出函数的导数，计算导数的规律性，即可得到结论．
解答 解：∵f0（x）=cosxsinx，
∴f1（x）=f0′（x）=-sin2x+cos2x=cos2x，
∴f2（x）=f1′（x）=-2sin2x，
∴f3（x）=f2′（x）=-22cos2x，
∴f4（x）=f3′（x）=23sin2x，
∴f5（x）=f4′（x）=24cos2x，
于是可知f2016（x）=22015sin2x．
点评 本题主要考查导数的计算，根据导数的公式，得到导数的规律是解决本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
11．
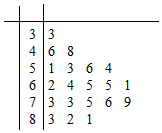某公司做了用户对其产品満意度的问卷调查，随机抽取了20名用户的评分，得到图所示茎叶图，对不低于75的评分，认为用户对产品满意，否则，认为不满意
（1）根据以上资料完成下面的2×2列联表，若据此数据算得K2=3.7781，则在犯错的概率不超过5%的前提下，你是否认为“満意”与“否”与性别有有关？
附：
（2）以此“满意”的频率作为概率，求在3人中恰有2人满意的概率；
（3）从以上男性用户中抽取2人，女性用户中抽取1人，其中满意的人数为ξ，求ξ的分布列与数学期望．
某公司做了用户对其产品満意度的问卷调查，随机抽取了20名用户的评分，得到图所示茎叶图，对不低于75的评分，认为用户对产品满意，否则，认为不满意（1）根据以上资料完成下面的2×2列联表，若据此数据算得K2=3.7781，则在犯错的概率不超过5%的前提下，你是否认为“満意”与“否”与性别有有关？
附：
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P（K2≥k） | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
（3）从以上男性用户中抽取2人，女性用户中抽取1人，其中满意的人数为ξ，求ξ的分布列与数学期望．
9．函数y=-3sin3x的最大值与取得最大值时相应的一个x的值为（ ）
| A． | 1，$\frac{π}{2}$ | B． | 1，-$\frac{π}{2}$ | C． | 3，$\frac{π}{6}$ | D． | 3，-$\frac{π}{6}$ |
13．下列函数是偶函数，且最小正周期为π的是（ ）
| A． | y=sin（π-2x） | B． | y=sin2xcos2x | C． | y=cos22x+1 | D． | y=cos（2x-π） |