题目内容
11.等比数列{an}的前n项和为Sn,若S3=2,S6=10.则S9等于42.分析 由等比数列{an}的性质可得:S3,S6-S3=2,S9-S6也成等比数列,即可得出.
解答 解:由等比数列{an}的性质可得:S3,S6-S3=2,S9-S6也成等比数列,
∴$({S}_{6}-{S}_{3})^{2}$=S3•(S9-S6),S3=2,S6=10.
∴(10-2)2=2×(S9-10),
解得S9=42.
故答案为:42.
点评 本题考查了等比数列的前n项和的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1.已知等差数列{an}公差为d,前n项和{sn},则下列描述不一定正确的是( )
| A. | 若a1>0,d>0,则n唯一确定时$s_n^{\;}$也唯一确定 | |
| B. | 若a1>0,d<0,则n唯一确定时$s_n^{\;}$也唯一确定 | |
| C. | 若a1>0,d>0,则$s_n^{\;}$唯一确定时n也唯一确定 | |
| D. | 若a1>0,d<0,则$s_n^{\;}$唯一确定时n也唯一确定 |
20.执行下面的程序框图,则输出的n的值为( )
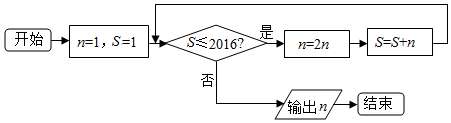

| A. | 10 | B. | 11 | C. | 1024 | D. | 2048 |
3.已知集合U=[0,5],A={x|x2-2x-3<0,x∈N},B=(0,1)∪(1,3)∪(3,5),则A∩(∁RB)=( )
| A. | {0,1,2) | B. | {-1,0,1,2,3} | C. | {0,1} | D. | {2} |