题目内容
11.直角坐标P(-1,1)的极坐标为(ρ>0,0<θ<π)$(\sqrt{2},\frac{3π}{4})$.分析 利用ρ=$\sqrt{{x}^{2}+{y}^{2}}$,tanθ=$\frac{y}{x}$,且0<θ<π,即可得出点P的极坐标.
解答 解:ρ=$\sqrt{(-1)^{2}+{1}^{2}}$=$\sqrt{2}$,tanθ=$\frac{1}{-1}$=-1,且0<θ<π,∴θ=$\frac{3π}{4}$.
∴点P的极坐标为$(\sqrt{2},\frac{3π}{4})$.
故答案为:$(\sqrt{2},\frac{3π}{4})$.
点评 本题考查了直角坐标与极坐标的互化,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.对于任意的实数a,b,c,下列命题正确的是( )
| A. | 若a>b,c=0,则ac>bc | B. | 若ac2>bc2,则a>b | ||
| C. | 若a>b,则$\frac{1}{a}$>$\frac{1}{b}$ | D. | 若a>b,则ac2>bc2 | ||
| E. | 若a>b,则ac2>bc2 |
19.已知向量$\overrightarrow a$=(-1,-2),$\overrightarrow b$=(1,λ),若$\overrightarrow a$,$\overrightarrow b$的夹角为钝角,则λ的取值范围是( )
| A. | (-∞,-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,2)∪(2,+∞) | C. | (-$\frac{1}{2}$,+∞) | D. | (2,+∞) |
3.下列积分值为2的是( )
| A. | ${∫}_{0}^{1}$2xdx | B. | ∫01exdx | C. | ${∫}_{1}^{e}$$\frac{1}{x}$dx | D. | ∫0πsinxdx |
20.已知定义在[-1,+∞]上的函数在区间[-1,3)上的解析式为f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}}(-1≤x<1)}\\{\frac{3}{2}-\frac{3}{x}×|x-2|(1≤x<3)}\end{array}\right.$,当x≥3时,函数满足f(x)=f(x-4)+1,若函数g(x)=f(x)-kx-k有6个零点,则实数k的取值或取值范围为( )
| A. | ($\frac{5}{14}$,$\frac{9+\sqrt{21}}{40}$) | B. | $\frac{5}{14}$ | C. | ($\frac{5}{12}$,$\frac{1}{2}$) | D. | ($\frac{5}{14}$,$\frac{5}{12}$) |
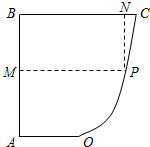 如图所示,已知AB⊥BC,OA∥BC,且AB=BC=2OA=4,曲线段OC是以点O为顶点且对称轴与AB平行的抛物线的一段.设P是曲线段OC上任意一点,点M在AB上,点N在BC上,PMBN是矩形,问点P在曲线段OC上什么位置的时候才能使矩形PMBN的面积最大?并求出最大面积.
如图所示,已知AB⊥BC,OA∥BC,且AB=BC=2OA=4,曲线段OC是以点O为顶点且对称轴与AB平行的抛物线的一段.设P是曲线段OC上任意一点,点M在AB上,点N在BC上,PMBN是矩形,问点P在曲线段OC上什么位置的时候才能使矩形PMBN的面积最大?并求出最大面积.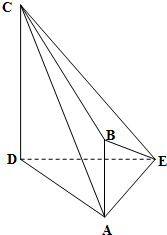 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.