题目内容
6.设曲线y=2015xn+1(n∈N*)在点(1,2015)处的切线与x轴的交点的横坐标为xn,令an=log2015xn,则a1+a2+…a2014的值为-1.分析 根据题设条件,利用导数先求出切线方程,进而求出xn,从而得到an,再由对数的运算法则能求出结果.
解答 解:∵曲线y=2015xn+1(n∈N*),
∴y′=2015(n+1)xn,
∴y′|x=1=2015(n+1),
∴曲线y=2015xn+1(n∈N*)在点(1,2015)处的切线方程为:
y-2015=2015(n+1)(x-1),
令y=0,解得切线与x轴的交点的横坐标为xn=x=$\frac{n}{n+1}$,
∵an=log2015xn=log2015$\frac{n}{n+1}$,
∴a1+a2+…+a2014
=log2015$\frac{1}{2}$+log2015$\frac{2}{3}$+…+log2015$\frac{2014}{2015}$
=log2015($\frac{1}{2}$×$\frac{2}{3}$×…×$\frac{2014}{2015}$)
=-1.
故答案为:-1.
点评 本题考查数列求和,涉及到导数、对数、数列等知识点,是一道构思巧妙的好题.

练习册系列答案
相关题目
14.已知随机变量X~N(0,σ2),且P(X>2)=0.4,则P(-2≤X≤0)=( )
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.8 |
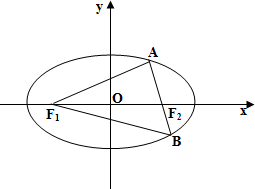 设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,离心率e=$\frac{1}{2}$,F1,F2分别为左、右焦点,AB是过右焦点的弦.
设椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的一个焦点与抛物线y2=4x的焦点重合,离心率e=$\frac{1}{2}$,F1,F2分别为左、右焦点,AB是过右焦点的弦.