题目内容
20.已知函数f(x)=x(m+e-x),其中e为自然对数的底数,曲线y=f(x)上存在不同的两点,使得曲线在这两点处的切线都与y轴垂直,则实数m的取值范围是( )| A. | (0,e-2) | B. | (e-2,+∞) | C. | (0,e2) | D. | (e2,+∞) |
分析 转化条件为函数有两个极值,通过导函数为0,推出m的表达式,转化两个函数的图象由两个交点,利用导函数的单调性,求出函数的值域,转化求解m的范围即可.
解答 解:曲线y=f(x)上存在不同的两点,使得曲线在这两点处的切线都与y轴垂直,等价于函数f(x)由两个不同极值,即f′(x)=0有两个不相同的实数根,令f′(x)=m+e-x-xe-x=0,可得m=$\frac{x-1}{{e}^{x}}$,令g(x)=$\frac{x-1}{{e}^{x}}$,则条件转化为直线y=m与y=g(x)有两个不同交点,
g′(x)=$\frac{{e}^{x}-(x-1){e}^{x}}{{e}^{2x}}$=$\frac{2-x}{{e}^{x}}$,
当x=2时,g′(x)=0,
当x>2时,g′(x)<0,g(x)是增函数;
当x<2时,g′(x)>0,g(x)是减函数;
所以x=2时,函数有极大值也是最大值,g(2)=e-2,x→-∞时,g(x)→-∞,x→+∞时,g(x)→0,
从而m∈(0,e-2).
故选:A.
点评 本题考查函数的单调性以及函数的极值的关系,考查转化思想以及分析问题解决问题的能力.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
12.阅读如图的程序框图,运行相应的程序,若输入N的值为19,则输出N的值为( )
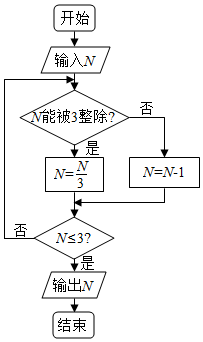

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
15.设函数f(x)=x3+3x2+6x+14且f(a)=1,f(b)=19.则a+b=( )
| A. | 2 | B. | 1 | C. | 0 | D. | -2 |
12.已知数列{an}满足a1=1,an+1=an2+an,设bn=$\frac{1}{{a}_{n}+1}$,用[x]表示不超过x的最大整数,则[b1+b2+…+b8]的值为( )
| A. | 1 | B. | 0 | C. | 2 | D. | 8 |
10.已知命题p:“?x0∈R,e${\;}^{{x}_{0}}$-x0-1≤0”,则¬p为( )
| A. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1≥0 | B. | ?x0∈R,e${\;}^{{x}_{0}}$-x0-1>0 | ||
| C. | ?x∈R,ex-x-1>0 | D. | ?x∈R,ex-x-1≥0 |