题目内容
20．已知-π＜x＜0，sinx+cosx=$\frac{1}{5}$，（1）求sinx-cosx的值；
（2）求$\frac{{2{{sin}^2}x+2sinx•cosx}}{1-tanx}$的值．
分析 （1）根据-π＜x＜0，判断sinx、cosx的值的正负，sin2x+cos2x=1，即可计算．
（2）根据sinx、cosx的值带入，即可求解．
解答 解：∵-π＜x＜0，
当$-π＜x≤-\frac{π}{2}$时，
可知sinx＜0、cosx＜0．
∴sinx+cosx=$\frac{1}{5}$不成立．
当$-\frac{π}{2}$＜x＜0时，
可知sinx＜0、cosx＞0．
∵sinx+cosx=$\frac{1}{5}$，sin2x+cos2x=1．
∴sinx=$-\frac{3}{5}$，cosx=$\frac{4}{5}$．tanx=$\frac{sinx}{cosx}=-\frac{3}{4}$．
（1）sinx-cosx=$-\frac{3}{5}-\frac{4}{5}=-\frac{7}{5}$．
（2）$\frac{{2{{sin}^2}x+2sinx•cosx}}{1-tanx}$=$\frac{2×\frac{9}{25}-2×\frac{3}{5}×\frac{4}{5}}{1+\frac{3}{4}}$=$-\frac{24}{175}$．
点评 本题考查了同角三角函数基本关系式，考查了计算能力，属于基础题．
练习册系列答案
相关题目
6．首项为-12的等差数列，从第10项起开始为正数，则公差d的取值范围是（ ）
| A． | d＞$\frac{8}{3}$ | B． | d＜3 | C． | $\frac{8}{3}$≤d＜3 | D． | $\frac{4}{3}$＜d≤$\frac{3}{2}$ |
15．6个电子产品中有2个次品，4个合格品，每次从中任取一个测试，测试完后不放回，直到两个次品都找到为止，那么测试次数X的均值为（ ）
| A． | $\frac{17}{15}$ | B． | $\frac{11}{15}$ | C． | $\frac{5}{3}$ | D． | $\frac{64}{15}$ |
5．已知三棱锥P-A BC四个顶点都在半径为2的球面上，PA⊥面ABC，PA=2，底面ABC是正三角形，点E是线段AB的中点，过点E作球O的截面，则截面面积的最小值是（ ）
| A． | $\frac{7π}{4}$ | B． | 2π | C． | $\frac{9π}{4}$ | D． | 3π |
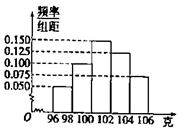某工厂对一批产品进行了抽样检测，如图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），（104，106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是（ ）