题目内容
11.如果直线y=ax+2与直线y=3x-b关于直线y=x对称,那么a+b=$\frac{19}{3}$.分析 由直线y=ax+2,解得(a≠0)x=$\frac{y-2}{a}$,把x与y互换可得:y=$\frac{1}{a}x-\frac{2}{a}$.根据直线y=ax+2与直线y=3x-b关于直线y=x对称,可得3=$\frac{1}{a}$,-$\frac{2}{a}$=-b,解得a,b.
解答 解:由直线y=ax+2,解得(a≠0)x=$\frac{y-2}{a}$,把x与y互换可得:y=$\frac{1}{a}x-\frac{2}{a}$.
∵直线y=ax+2与直线y=3x-b关于直线y=x对称,
∴3=$\frac{1}{a}$,-$\frac{2}{a}$=-b,解得a=$\frac{1}{3}$,b=6.
∴a+b=$\frac{19}{3}$.
故答案为:$\frac{19}{3}$.
点评 本题考查了直线方程、对称性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.在梯形ABCD中,$\overrightarrow{AB}+3\overrightarrow{CD}=\overrightarrow 0$,则$\overrightarrow{BC}$等于( )
| A. | $-\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | B. | $-\frac{2}{3}\overrightarrow{AB}+\frac{4}{3}\overrightarrow{AD}$ | C. | $\frac{2}{3}\overrightarrow{AB}-\overrightarrow{AD}$ | D. | $-\frac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}$ |
6.首项为-12的等差数列,从第10项起开始为正数,则公差d的取值范围是( )
| A. | d>$\frac{8}{3}$ | B. | d<3 | C. | $\frac{8}{3}$≤d<3 | D. | $\frac{4}{3}$<d≤$\frac{3}{2}$ |
16.已知随机变量ξ服从正态分布N(1,σ2).若P(0<ξ≤1)=0.4,则P(ξ≥2)=( )
| A. | 0.4 | B. | 0.3 | C. | 0.2 | D. | 0.1 |
5.已知三棱锥P-A BC四个顶点都在半径为2的球面上,PA⊥面ABC,PA=2,底面ABC是正三角形,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是( )
| A. | $\frac{7π}{4}$ | B. | 2π | C. | $\frac{9π}{4}$ | D. | 3π |
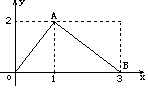 函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),
函数f(x)的图象是如图所示的折线段OAB,点A坐标为(1,2),点B坐标为(3,0),