题目内容
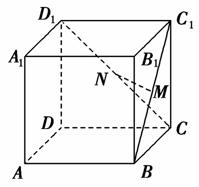
如图所示,在正方体AC1中,M、N分别是A1B1、BB1的中点,求异面直线AM和CN所成角的余弦值.
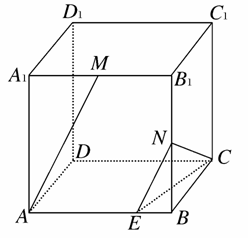
[解析] 在平面ABB1A1内作EN∥AM交AB于E,则EN与CN所成的锐角(或直角)即为AM和CN所成的角.设正方体棱长为a.
在△CNE中,可求得CN= a,NE=
a,NE= a,CE=
a,CE= a,由余弦定理得,cos∠CNE=
a,由余弦定理得,cos∠CNE= =
= .
.
即异面直角AM与CN所成角的余弦值为 .
.
(2)利用平行平面平移直线构成可解的三角形,是求异面直线所成角的途径之二;
这种方法常见于两条异面直线分别在两个互相平行的平面内,可利用面面平行的性质,将一条直线平移到另一条所在的平面内.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
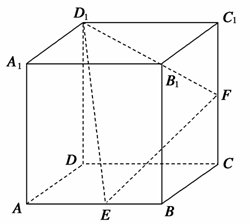
 AD,∠BAD=60°,E、F分别为AD、PC的中点.
AD,∠BAD=60°,E、F分别为AD、PC的中点.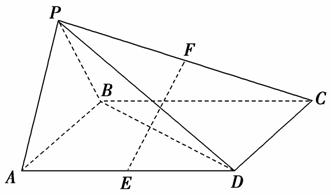
 ,P是BC1上一动点,如图所示,则CP+PA1的最小值为________.
,P是BC1上一动点,如图所示,则CP+PA1的最小值为________.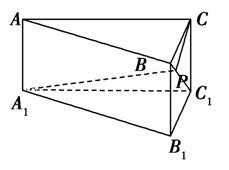
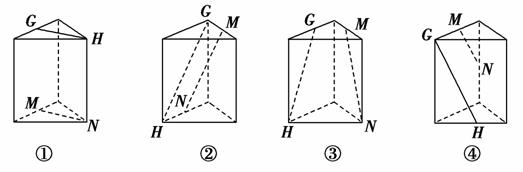
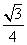 a2 B.
a2 B.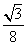 a2 C.
a2 C.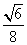 a2 D.
a2 D.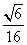 a2
a2