题目内容
1.设点P为有公共焦点F1、F2的椭圆M和双曲线Γ的一个交点,$cos∠{F_1}P{F_2}=\frac{4}{5}$,椭圆M的离心率为e1,双曲线Γ的离心率为e2.若e2=2e1,则e1=$\frac{{\sqrt{130}}}{20}$.分析 由椭圆及双曲线的定义可知m+n=2a1,m-n=2a2.利用余弦定理,求得10=$\frac{1}{{e}_{1}^{2}}$+$\frac{9}{{e}_{2}^{2}}$,将e2=2e1,即可求得e1.
解答 解:设椭圆与双曲线的半长轴分别为a1,a2,半焦距为c.e1=$\frac{c}{{a}_{1}}$,e2=$\frac{c}{{a}_{2}}$.
设|PF1|=m,|PF2|=n,不妨设m>n,
则m+n=2a1,m-n=2a2.
∴m2+n2=2${a}_{1}^{2}$+2${a}_{2}^{2}$,mn=${a}_{1}^{2}$-${a}_{2}^{2}$
4c2=m2+n2-2mncos∠F1PF2,
∴4c2=2${a}_{1}^{2}$+2${a}_{2}^{2}$-2(${a}_{1}^{2}$-${a}_{2}^{2}$)×$\frac{4}{5}$.
整理得:10c2=${a}_{1}^{2}$+9${a}_{2}^{2}$,
∴10=$\frac{1}{{e}_{1}^{2}}$+$\frac{9}{{e}_{2}^{2}}$,又e2=2e1,
∴40${e}_{1}^{2}$=13,e1∈(0,1).
解得:e1=$\frac{{\sqrt{130}}}{20}$.
∴椭圆的离心率e1=$\frac{{\sqrt{130}}}{20}$.
故答案为:$\frac{{\sqrt{130}}}{20}$.
点评 本题考查双曲线及椭圆的离心率公式,考查余弦定理的应用,考查计算能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
11.a、b均为实数,则a<b<0是a2>b2的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.已知椭圆:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<3),左右焦点分别为F1,F2,过F1的直线l交椭圆于A、B两点,若|BF2|+|AF2|的最大值为10,则b的值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
13.函数y=sin2(x-$\frac{π}{4}$)的图象沿x轴向右平移m个单位(m>0),所得图象关于y轴对称,则m的最小值为( )
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
10.设等差数列{an}的公差为d,d≠0,若{an}的前10项之和大于其前21项之和,则( )
| A. | d<0 | B. | d>0 | C. | a16<0 | D. | a16>0 |
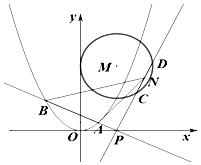 如图,抛物线E:x2=2py(p>0)的焦点为(0,1),圆心M在射线y=2x(x≥0)上且半径为2的圆M与y轴相切.
如图,抛物线E:x2=2py(p>0)的焦点为(0,1),圆心M在射线y=2x(x≥0)上且半径为2的圆M与y轴相切.