题目内容
已知f(x)是二次函数,不等式f(x)<0的解集是(0,5),且f(x)在区间[-2,4]上的最大值是28.
(1)求f(x)的解析式;
(2)设函数f(x)在x∈[t,t+1]上的最小值为g(t),求g(t)的表达式.
(1)求f(x)的解析式;
(2)设函数f(x)在x∈[t,t+1]上的最小值为g(t),求g(t)的表达式.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:综合题,函数的性质及应用
分析:(1)根据题意,设f(x)=ax(x-5)(a>0),可得函数图象的对称轴x=2.5,恰好位于区间[-2,4],得f(x)的最大值是f(-2)=14a=28,得a=2,可得函f(x)数的表达式;
(2)分t+1≤2.5时、t≥2.5时和1.5<t<2.5时三种情况,分别讨论函数的单调性,可得相应情况下函数的最小值,最后综合可得g(t)的表达式.
(2)分t+1≤2.5时、t≥2.5时和1.5<t<2.5时三种情况,分别讨论函数的单调性,可得相应情况下函数的最小值,最后综合可得g(t)的表达式.
解答:
解:(1)∵f(x)是二次函数,且f(x)<0的解集是(0,5),
∴可设f(x)=ax(x-5)(a>0).
∴f(x)在区间[-2,4]上的最大值是f(-2)=14a.
由已知,得14a=28,∴a=2,∴f(x)=2x(x-5)=2x2-10x(x∈R).
(2)由(1)得f(x)=2(x-2.5)2-12.5,函数图象的开口向上,对称轴为x=2.5
①当t+1≤2.5时,即t≤1.5时,f(x)在[t,t+1]上单调递减,
此时f(x)的最小值g(t)=f(t+1)=2(t+1)2-10(t+1)=2t2-6t-8;
②当t≥2.5时,f(x)在[t,t+1]上单调递增,
此时f(x)的最小值g(t)=f(t)=2t2-10t;
③当1.5<t<2.5时,函数y=f(x)在对称轴处取得最小值
此时,g(t)=f(2.5)=-12.5
综上所述,得g(t)的表达式为:g(t)=
.
∴可设f(x)=ax(x-5)(a>0).
∴f(x)在区间[-2,4]上的最大值是f(-2)=14a.
由已知,得14a=28,∴a=2,∴f(x)=2x(x-5)=2x2-10x(x∈R).
(2)由(1)得f(x)=2(x-2.5)2-12.5,函数图象的开口向上,对称轴为x=2.5
①当t+1≤2.5时,即t≤1.5时,f(x)在[t,t+1]上单调递减,
此时f(x)的最小值g(t)=f(t+1)=2(t+1)2-10(t+1)=2t2-6t-8;
②当t≥2.5时,f(x)在[t,t+1]上单调递增,
此时f(x)的最小值g(t)=f(t)=2t2-10t;
③当1.5<t<2.5时,函数y=f(x)在对称轴处取得最小值
此时,g(t)=f(2.5)=-12.5
综上所述,得g(t)的表达式为:g(t)=
|
点评:本题给出一元二次不等式的解集,求二次函数的表达式并求它在闭区间上的最小值,着重考查了二次函数的图象与性质、不等式的解法等知识,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 在三棱锥P-ABC中,△ABC为正三角形,∠PCA=90°,D为PA中点,二面角P-AC-B的大小为为120°,PC=2,AB=2
在三棱锥P-ABC中,△ABC为正三角形,∠PCA=90°,D为PA中点,二面角P-AC-B的大小为为120°,PC=2,AB=2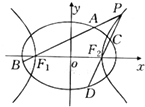 如图,已知以F1(-2,0),F2(2,0)为焦点的椭圆上有点Q,三角形QF1F2的周长为4(
如图,已知以F1(-2,0),F2(2,0)为焦点的椭圆上有点Q,三角形QF1F2的周长为4( 如图,边长为3的正方形ABCD中,点E,F分别为边AB,BC上的点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.
如图,边长为3的正方形ABCD中,点E,F分别为边AB,BC上的点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′.