题目内容
四根长都为2的直铁条，若再选两根长都为a的直铁条，使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架，求能形成的三棱锥体积最大值．
考点：棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：根据条件，四根长为2的直铁条与两根长为a的直铁条要组成三棱镜形的铁架，有以下两种情况：①底面是边长为2的正三角形，三条侧棱长为2，a，a；②构成三棱锥的两条对角线长为a，其他各边长为2．当①中，SA⊥平面ABC时，三棱锥体积取最大值．
解答：
解：根据条件，四根长为2的直铁条与两根长为a的直铁条要组成三棱镜形的铁架，
有以下两种情况：
①底面是边长为2的正三角形，
三条侧棱长为2，a，a，如图，
此时a可以取最大值，可知AD=
，
SD=
，
则有
＜2+
，
即a2＜8+4
=（
+
）2，
即有1＜a＜
+
．
②构成三棱锥的两条对角线长为a，其他各边长为2，
如图所示，此时0＜a＜2
．
∴当①中，SA⊥平面ABC时，三棱锥体积取最大值，
此时VS-ABC=
×SA×S△ABC=
×2×
×2×2×sin60°=
有以下两种情况：
①底面是边长为2的正三角形，
三条侧棱长为2，a，a，如图，
此时a可以取最大值，可知AD=
| 3 |
SD=
| a2-1 |
则有
| a2-1 |
| 3 |
即a2＜8+4
| 3 |
| 6 |
| 2 |
即有1＜a＜
| 6 |
| 2 |
②构成三棱锥的两条对角线长为a，其他各边长为2，
如图所示，此时0＜a＜2
| 2 |
∴当①中，SA⊥平面ABC时，三棱锥体积取最大值，
此时VS-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
点评：本题考查的知识点是空间想像能力，我们要结合分类讨论思想，数形结合思想，极限思想，求出a的最大值和最小值，进而得到形成的三棱锥体积最大值．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
已知函数f（x）=
则f（4）等于（ ）
|
| A、16 | B、0 | C、2 | D、8 |
已知向量
=（1，1，0），
=（-1，0，2），且k
+
与
互相垂直，则k的值是（ ）
| a |
| b |
| a |
| b |
| b |
| A、-5 | ||
B、
| ||
C、
| ||
| D、5 |
如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD的边BC垂直于圆O所在的平面．
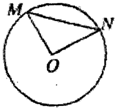如图，M是半径R的圆周上一个定点，在圆周上等可能的任取一点N，连接MN，则弦MN的长度超过| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|