题目内容
18.已知a>0,b>0,a2+b2-6a=0,则ab的最大值为( )| A. | $\frac{{27\sqrt{3}}}{4}$ | B. | 9 | C. | $\frac{81}{4}$ | D. | $\frac{27}{4}$ |
分析 根据题意可得9=(a-3)2+b2,设a=3cosθ+3,b=3sinθ,根据二倍角公式和同角的三角函数的关系可得ab=36(1-sin2$\frac{θ}{2}$)${\;}^{\frac{3}{2}}$sin$\frac{θ}{2}$,设sin$\frac{θ}{2}$=x,则0<x<1,令f(x)=(1-x2)${\;}^{\frac{3}{2}}$•x,根据导数和函数最值得关系求出最大值即可.
解答 解:∵a>0,b>0,配方为9=(a-3)2+b2,
设a=3cosθ+3,b=3sinθ,
∴ab=(3cosθ+3)•3sinθ=9×2cos2$\frac{θ}{2}$•2sin$\frac{θ}{2}$cos$\frac{θ}{2}$
=36(cos2$\frac{θ}{2}$)${\;}^{\frac{3}{2}}$sin$\frac{θ}{2}$=36(1-sin2$\frac{θ}{2}$)${\;}^{\frac{3}{2}}$sin$\frac{θ}{2}$,
再设sin$\frac{θ}{2}$=x,则0<x<1
令f(x)=(1-x2)${\;}^{\frac{3}{2}}$•x,
∴f′(x)=(1-x2)${\;}^{\frac{1}{2}}$((1-4x2),
令f′(x)=0,解得x=$\frac{1}{2}$,
当0<x<$\frac{1}{2}$,f′(x)>0,函数f(x)单调递增,
当$\frac{1}{2}$<x<1,f′(x)<0,函数f(x)单调递减,
∴f(x)max=f($\frac{1}{2}$)=(1-$\frac{1}{4}$)${\;}^{\frac{3}{2}}$•$\frac{1}{2}$=$\frac{3\sqrt{3}}{16}$,
∴ab的最大值为36×$\frac{3\sqrt{3}}{16}$=$\frac{27\sqrt{3}}{4}$
故选:A
点评 本题考查了导数和函数最值的关系,关键采用换元,本题两次换元,考查了学生的转化能力和运算能力,属于难题.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<a<b |
| A. | {x|-2≤x<0或3<x≤4} | B. | {x|-2≤x≤0或3≤x≤4} | C. | {x|-2<x≤4} | D. | {x|0<x<3} |
| A. | $\frac{π}{6}$,$\sqrt{2}$ | B. | $\frac{π}{4}$,2 | C. | $\frac{π}{3}$,$\sqrt{6}$ | D. | $\frac{3π}{4}$,2 |
| A. | (2016,2017) | B. | (2016,2017] | C. | [2016,2017) | D. | (-2016,2017) |
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{7}{3}$ | D. | 3 |
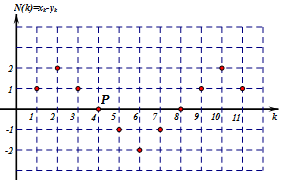 已知一个由11人组成的评审委员会以投票方式从符合要求的甲,乙两名候选人中选出一人参加一次活动.投票要求委员会每人只能选一人且不能弃选,每位委员投票不受他人影响.投票结果由一人唱票,一人统计投票结果.
已知一个由11人组成的评审委员会以投票方式从符合要求的甲,乙两名候选人中选出一人参加一次活动.投票要求委员会每人只能选一人且不能弃选,每位委员投票不受他人影响.投票结果由一人唱票,一人统计投票结果.