题目内容
5.已知函数f(x)是定义在R上的奇函数,且是以2为周期的周期函数,若当x∈[0,1)时,f(x)=2x-1,则f(${log_{\frac{1}{2}}}$5)的值为-$\frac{1}{4}$.分析 由题意可得:f(${log_{\frac{1}{2}}}$5)=f(-log25)=-f(log25).结合函数的周期性,根据题中的条件代入函数解析式可得答案.
解答 解:由题意可得:f(${log_{\frac{1}{2}}}$5)=f(-log25),
因为f(x)是定义在R上的奇函数,所以f(${log_{\frac{1}{2}}}$5)=-f(log25).
又因为f(x)是周期为2的周期函数,所以f(log25)=f(log25-2)=f(log2$\frac{5}{4}$).
因为0<log2$\frac{5}{4}$<1,并且当x∈[0,1)时,f(x)=2x-1,所以f(log25)=f(log2$\frac{5}{4}$)=$\frac{5}{4}$-1=$\frac{1}{4}$,
所以 f(${log_{\frac{1}{2}}}$5)=f(-log25)=-$\frac{1}{4}$.
故答案为:-$\frac{1}{4}$.
点评 本题主要考查函数的有关性质,如奇偶性、周期性,以及对数的有关运算性质,此题属于基础题型.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
15.已知实数x,y满足$\left\{\begin{array}{l}{x+y-4≤0}\\{y-1≥0}\\{x-1≥0}\end{array}\right.$,则z=$\frac{{y}^{2}}{x}$的最大值是 ( )
| A. | $\frac{1}{3}$ | B. | 9 | C. | 2 | D. | 11 |
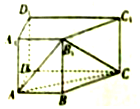 如图,在直四棱柱ABCD-A1B1C1D1中,AB∥DC,AA1=1,AB:AD:BC:DC=3:4:5:6,侧棱AA1⊥底面ABCD.
如图,在直四棱柱ABCD-A1B1C1D1中,AB∥DC,AA1=1,AB:AD:BC:DC=3:4:5:6,侧棱AA1⊥底面ABCD.