题目内容
15.若不等式${2^{2x-1}}+a>{log_{\frac{1}{2}}}x$在区间[1,2]上恒成立,则a的取值范围是( )| A. | a<-2 | B. | a>-2 | C. | a<-9 | D. | a>-9 |
分析 问题转化为a>-log2x-22x-1在[1,2]恒成立,令f(x)=-log2x-22x-1,x∈[1,2],求出f(x)的最大值,求出a的范围即可.
解答 解:若不等式${2^{2x-1}}+a>{log_{\frac{1}{2}}}x$在区间[1,2]上恒成立,
即a>-log2x-22x-1在[1,2]恒成立,
令f(x)=-log2x-22x-1,x∈[1,2],
显然f(x)在[1,2]递减,
故f(x)max=f(1)=-2,
故a>-2,
故选:B.
点评 本题考查了函数恒成立问题,考查对数函数以及指数函数的性质,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.数列{an}满足a1=$\sqrt{3}$与an+1=[an]+$\frac{1}{\{{a}_{n}\}}$([an]与{an}分别表示an的整数部分与分数部分),则a2017=( )
| A. | $3021+\sqrt{3}$ | B. | $3024+\sqrt{3}$ | C. | $3021+\frac{{\sqrt{3}-1}}{2}$ | D. | $3024+\frac{{\sqrt{3}-1}}{2}$ |
4.设向量$\overrightarrow{a}$=(2,3m+2),$\overrightarrow{b}$=(m,-1).若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数m等于( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
5.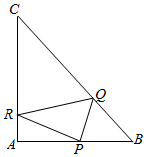 在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
 在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )| A. | 2 | B. | 1 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
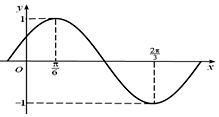 函数f(x)=Asin(ωx+φ)$({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示.
函数f(x)=Asin(ωx+φ)$({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示.