题目内容

14．在平面直角坐标系下，曲线C1：$\left\{\begin{array}{l}{x=2t+2a}\\{y=-t}\end{array}\right.$（t为参数），曲线C2：$\left\{\begin{array}{l}{x=2sinθ}\\{y=1+2cosθ}\end{array}\right.$（θ为参数），若曲线C1，C2有公共点，则实数a的取值范围是1-$\sqrt{5}$≤a≤1+$\sqrt{5}$．

分析 参数方程化为普通方程，利用圆心到直线的距离小于等于半径，即可得出结论．

解答 解：曲线C1：$\left\{\begin{array}{l}{x=2t+2a}\\{y=-t}\end{array}\right.$（t为参数），普通方程为x+2y-2a=0，
曲线C2：$\left\{\begin{array}{l}{x=2sinθ}\\{y=1+2cosθ}\end{array}\right.$（θ为参数），普通方程为x2+（y-1）2=4，
∵曲线C1，C2有公共点，
∴$\frac{|2-2a|}{\sqrt{5}}$≤2，
∴1-$\sqrt{5}$≤a≤1+$\sqrt{5}$，
故答案为1-$\sqrt{5}$≤a≤1+$\sqrt{5}$．

点评 本题考查参数方程化为普通方程，考查点到直线距离公式的运用，属于中档题．

练习册系列答案
相关题目
4．已知向量$\overrightarrow{a}$=$（\frac{1}{2}，\;\frac{{\sqrt{3}}}{2}）$，$\overrightarrow{b}$=$（-\frac{{\sqrt{3}}}{2}，\;\frac{1}{2}）$，则（$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{a}$=（　　）
A．-1B．0C．1D．2
5．小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制，5人坐成一排．若小明的父母至少有一人与他相邻，则不同坐法的总数为（　　）
A．60B．72C．84D．96
2．已知点A（1，0），B（3，0），若直线y=kx+1上存在点P，满足PA⊥PB，则k的取值范围是$[-\frac{4}{3}，0]$．
9．已知函数f（x）=2$\sqrt{3}$tan（$\frac{x}{2}$+$\frac{π}{4}$）cos2（$\frac{x}{2}$+$\frac{π}{4}$）-sin（x+π）．
（Ⅰ）求f（x）的定义域和最小正周期；
（Ⅱ）若将f（x）的图象向右平移$\frac{π}{6}$个单位，得到函数g（x）的图象，求函数g（x）在区间[0，π]上的最大值和最小值．
19．已知数列{an}的前n项和Sn=n2-n，正项等比数列{bn}中，b2=a3，bn+3bn-1=4bn2（n≥2，n∈N+），则log2bn=（　　）
A．nB．2n-1C．n-2D．n-1
6．已知△ABC内角A，B，C的对边分别是a，b，c，若cosB=$\frac{1}{4}$，b=2，sinC=2sinA，则△ABC的面积为（　　）
A．$\sqrt{15}$B．$\frac{\sqrt{15}}{2}$C．$\frac{\sqrt{15}}{6}$D．$\frac{\sqrt{15}}{4}$
8．图中，能表示函数y=f（x）的图象的是（　　）
A．B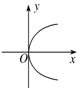．C．D．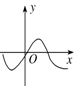
9．对任意实数a，b，c，d，定义符号$（\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}）$=$\left\{\begin{array}{l}{\sqrt{ad-bc}（ad≥bc）}\\{\frac{1}{2}\sqrt{bc-ad}（ad＜bc）}\end{array}\right.$，已知函数f（x）=$（\begin{array}{l}{x}&{4}\\{1}&{x}\end{array}）$，直线l：kx-y+3-2k=0，若直线l与函数f（x）的图象有两个公共点，则实数k的取值范围是（　　）
A．（-1，$\frac{2}{3}$）∪（$\frac{3}{4}$，1）B．（-1，$\frac{17}{24}$）C．（-1，$\frac{17}{24}$）∪（$\frac{3}{4}$，1）D．（-1，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网