题目内容
2.设函数f(x)=ex-|ln(-x)|的两个零点为x1,x2,则( )| A. | x1x2<0 | B. | x1x2=1 | C. | x1x2>1 | D. | 0<x1x2<1 |
分析 作出y=|ln(-x)|和y=ex在R上的图象,可知恰有两个交点,设零点为x1,x2,再结合零点存在定理,可得结论
解答 解:令f(x)=0,则|ln(-x)|=ex,
作出y=|ln(-x)|和y=ex在R上的图象,
可知恰有两个交点,设零点为x1,x2且|ln(-x1)|<|ln(-x2)|,x1<-1,x2>-1,
故有$\frac{1}{{x}_{1}}$>x2,即x1x2<1.
又由x1x2>0.
故0<x1x2<1
故选:D
点评 本题考查函数的零点与方程根的关系,考查数形结合的数学思想,考查学生分析解决问题的能力,正确作出函数图象是关键.

练习册系列答案
相关题目
10.设集合P={1,2,3,4},Q={x||x|≤3,x∈R},则P∩Q等于( )
| A. | {1} | B. | {1,2,3} | ||
| C. | {3,4} | D. | {-3,-2,-1,0,1,2,3} |
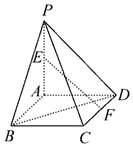 如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.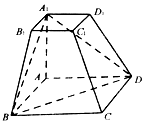 如图,在四棱台ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=2A1B1,AA1⊥平面ABCD.
如图,在四棱台ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=2A1B1,AA1⊥平面ABCD.