题目内容
14.已知数列{an}中,a1=1,a2=3,对任意n∈N*,an+2≤an+3•2n,an+1≥2an+1恒成立,则数列{an}的前n项和Sn=2n+1-n-2.分析 an+1≥2an+1,利用递推可得:an+1≥2an+1≥22an-1+2+1≥…≥2na1+2n-1+2n-2+…+2+1=2n+1-1,即an≥2n-1.(n=1时也成立).由an+2≤an+3•2n,即an+2-an≤3•2n,利用“累加求和”方法结合an+1≥2an+1,可得an≤2n-1,因此an=2n-1.即可得出.
解答 解:∵an+1≥2an+1,
∴an+1≥2an+1≥22an-1+2+1≥23an-2+22+2+1≥…≥2na1+2n-1+2n-2+…+2+1=$\frac{{2}^{n+1}-1}{2-1}$=2n+1-1,
∴an≥2n-1.(n=1时也成立).
由对任意n∈N*,an+2≤an+3•2n,即an+2-an≤3•2n,
∴a3-a1≤3×2,
a4-a2≤3×22,
…,
an-2-an-4≤3×2n-4
an-1-an-3≤3×2n-3,
an-an-2≤3×2n-2,
an+1-an-1≤3×2n-1.
∴an+1+an≤1+3+3×2+3×22+…+3×2n-2+3×2n-1=1+3×$\frac{{2}^{n}-1}{2-1}$=3×2n-2.(n≥2).
∵an+1≥2an+1,
∴3an+1≤3×2n-2.
∴an≤2n-1.
∴2n-1≤an≤2n-1,
∴an=2n-1,
∴数列{an}的前n项和Sn=$\frac{2({2}^{n}-1)}{2-1}$-n=2n+1-2-n.
故答案为:2n+1-n-2.
点评 本题考查了递推关系、不等式的性质、“累加求和”方法、等比数列的前n项和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
2.设函数f(x)=ex-|ln(-x)|的两个零点为x1,x2,则( )
| A. | x1x2<0 | B. | x1x2=1 | C. | x1x2>1 | D. | 0<x1x2<1 |
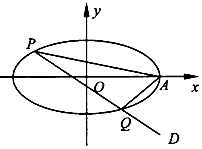 在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的焦距为2,离心率为$\frac{\sqrt{2}}{2}$,椭圆的右顶点为A.
在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的焦距为2,离心率为$\frac{\sqrt{2}}{2}$,椭圆的右顶点为A.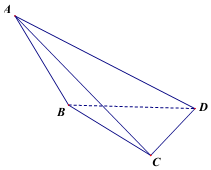 如图,等边三角形ABC与等腰直角三角形DBC公共边BC,BC=$\sqrt{2}$,DB=DC,AD=$\sqrt{3}$.
如图,等边三角形ABC与等腰直角三角形DBC公共边BC,BC=$\sqrt{2}$,DB=DC,AD=$\sqrt{3}$.