题目内容
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),过双曲线上任意一点P分别作斜率为-$\frac{b}{a}$和$\frac{b}{a}$的两条直线l1和l2,设直线l1与x轴、y轴所围成的三角形的面积为S,直线l2与x轴、y轴所围成的三角形的面积为T,则S•T的值为$\frac{{a}^{2}{b}^{2}}{4}$.分析 不妨设点P在第一象限,设点P(x0,y0),得到直线l1的方程为y-y0=-$\frac{b}{a}$(x-x0),直线l2的方程为y-y0=$\frac{b}{a}$(x-x0),再分别求出A,B,C,D的坐标,表示出S,T,计算ST即可.
解答 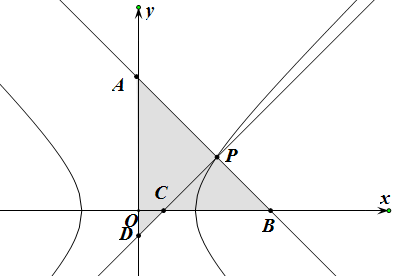 解:不妨设点P在第一象限,设点P(x0,y0)
解:不妨设点P在第一象限,设点P(x0,y0)
∴直线l1的方程为
y-y0=-$\frac{b}{a}$(x-x0),
直线l2的方程为
y-y0=$\frac{b}{a}$(x-x0),
∴A(0,y0+$\frac{b}{a}$x0),
B(x0+$\frac{a}{b}$x0,0),
D(0,y0-$\frac{b}{a}$x0),
C(x0-$\frac{a}{b}$y0,0),
∴S=$\frac{1}{2}$(y0+$\frac{b}{a}$x0)(x0+$\frac{a}{b}$x0),T=-$\frac{1}{2}$(y0-$\frac{b}{a}$x0)(x0-$\frac{a}{b}$y0),
∴ST=-$\frac{1}{4}$(y02-$\frac{b}{a}$x02)(x02-$\frac{a}{b}$y02)=$\frac{{a}^{2}{b}^{2}}{4}$,
故答案为:$\frac{{a}^{2}{b}^{2}}{4}$
点评 本题考查双曲线的标准方程,以及双曲线的简单性质的应用,比较基础.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
2.设函数f(x)=ex-|ln(-x)|的两个零点为x1,x2,则( )
| A. | x1x2<0 | B. | x1x2=1 | C. | x1x2>1 | D. | 0<x1x2<1 |
16.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )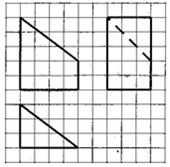

| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
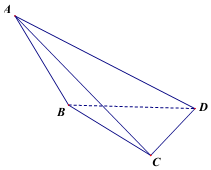 如图,等边三角形ABC与等腰直角三角形DBC公共边BC,BC=$\sqrt{2}$,DB=DC,AD=$\sqrt{3}$.
如图,等边三角形ABC与等腰直角三角形DBC公共边BC,BC=$\sqrt{2}$,DB=DC,AD=$\sqrt{3}$.