题目内容
12.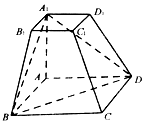 如图,在四棱台ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=2A1B1,AA1⊥平面ABCD.
如图,在四棱台ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=2A1B1,AA1⊥平面ABCD.(1)求证:BD⊥C1C;
(2)求证:C1C∥平面A1BD.
分析 (1)由AA1⊥平面ABCD,可证AA1⊥BD.四边形ABCD是菱形可得AC⊥BD,由线面垂直的判定定理可证BD⊥面ACC1A1,再由线面垂直的性质定理可证BD⊥CC1.
(2)连接AC和A1C1,设AC∩BD=E,先证明四边形ECC1A1为平行四边形,可得CC1∥A1E,再由线面平行的判定定理可证CC1∥平面A1BD.
解答 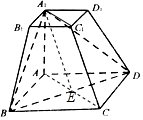 证明:(1)∵AA1⊥平面ABCD,
证明:(1)∵AA1⊥平面ABCD,
∴AA1⊥BD.
∵四边形ABCD是菱形,∴AC⊥BD,
又 AC∩AA1=A,∴BD⊥面ACC1A1.
由CC1?面ACC1A1,
∴BD⊥CC1.
(2)连接AC和A1C1,设 AC∩BD=E,由于底面ABCD是平行四边形,故E为平行四边形ABCD的
中心,由棱台的定义及AB=2AD=2A1B1,可得 EC∥A1C1,且 EC=A1C1,
故ECC1A1为平行四边形,∴CC1∥A1E,而CC1?平面A1BD,A1E?平面A1BD,
∴CC1∥平面A1BD.
点评 本题考查线面平行、垂直的判定定理、线面平行、垂直的性质定理的应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
2.设函数f(x)=ex-|ln(-x)|的两个零点为x1,x2,则( )
| A. | x1x2<0 | B. | x1x2=1 | C. | x1x2>1 | D. | 0<x1x2<1 |
7.若正数x,y满足$\frac{1}{y}+\frac{3}{x}=1$,则3x+4y的最小值是( )
| A. | 24 | B. | 28 | C. | 25 | D. | 26 |
17.已知实数x,y满足$\left\{\begin{array}{l}x≥0\\ y≥0\\ \frac{x}{3}+\frac{y}{4}≤1\end{array}\right.$,则$\frac{x+2y+3}{x+1}$的取值范围是( )
| A. | $[\frac{2}{3},11]$ | B. | [3,11] | C. | $[\frac{3}{2},11]$ | D. | [1,11] |
2.若直线ax+y=0截圆x2+y2-2x-6y+6=0所得的弦长为$2\sqrt{3}$,则实数a=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
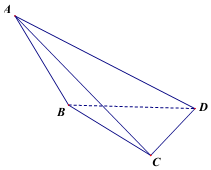 如图,等边三角形ABC与等腰直角三角形DBC公共边BC,BC=$\sqrt{2}$,DB=DC,AD=$\sqrt{3}$.
如图,等边三角形ABC与等腰直角三角形DBC公共边BC,BC=$\sqrt{2}$,DB=DC,AD=$\sqrt{3}$.