题目内容
17.已知命题p:?x∈R,不等式x2-mx+$\frac{3}{2}$>0恒成立,命题q:椭圆$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{3-m}$=1的焦点在x轴上.若命题p∨q为真命题,求实数m的取值范围(-$\sqrt{6}$,3).分析 先求出命题p,q为真时,m的取值范围,求其并集可得答案.
解答 解:若?x∈R,不等式x2-mx+$\frac{3}{2}$>0恒成立,
则△=m2-6<0,
解得:m∈(-$\sqrt{6}$,$\sqrt{6}$);
即命题p:m∈(-$\sqrt{6}$,$\sqrt{6}$);
若椭圆$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{3-m}$=1的焦点在x轴上.
则m-1>3-m>0,
解得:m∈(2,3),
即命题p:m∈(2,3),
若命题p∨q为真命题,则m∈(-$\sqrt{6}$,3),
故答案为:(-$\sqrt{6}$,3).
点评 本题以命题的真假判断与应用为载体,考查了复合命题,不等式恒成立,椭圆的标准方程等知识点,难度中档.

练习册系列答案
相关题目
2.设函数f(x)=ex-|ln(-x)|的两个零点为x1,x2,则( )
| A. | x1x2<0 | B. | x1x2=1 | C. | x1x2>1 | D. | 0<x1x2<1 |
7.若正数x,y满足$\frac{1}{y}+\frac{3}{x}=1$,则3x+4y的最小值是( )
| A. | 24 | B. | 28 | C. | 25 | D. | 26 |
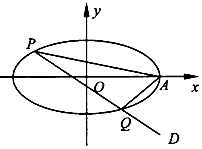 在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的焦距为2,离心率为$\frac{\sqrt{2}}{2}$,椭圆的右顶点为A.
在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的焦距为2,离心率为$\frac{\sqrt{2}}{2}$,椭圆的右顶点为A.