题目内容
16.一个正方体内接于高为$\sqrt{2}$m,底面半径为1m的圆锥中,则正方体的棱长是( )| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 作出过正方体的体对角线作圆锥的轴截面,设正方体的棱长为x,通过三角形相似,求出正方体的棱长即可.
解答  解:如图,过正方体的体对角线作圆锥的轴截面,设正方体的棱长为x,
解:如图,过正方体的体对角线作圆锥的轴截面,设正方体的棱长为x,
则OC=$\frac{\sqrt{2}}{2}$x,∴$\frac{\frac{\sqrt{2}}{2}x}{1}$=$\frac{\sqrt{2}-x}{\sqrt{2}}$,
解得x=$\frac{\sqrt{2}}{2}$,
∴正方体的棱长为$\frac{\sqrt{2}}{2}$,
故选:B.
点评 本题是中档题,正确作出图形,注意到过正方体的体对角线作圆锥的轴截面,AC是正方体的面对角线,三角形相似.考查空间想象能力,计算能力好题,常考题型.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
7.椭圆$\frac{x^2}{5}+\frac{y^2}{3}=1$的离心率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
11.“x-3=0”是“(x-3)(x+4)=0”的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分又不必要 |
8.若变量x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤4\\ y≥1\end{array}\right.$,则z=$\frac{1}{2}$x+y的取值范围为( )
| A. | $[\frac{3}{2},3]$ | B. | $[\frac{3}{2},\frac{5}{2}]$ | C. | $[\frac{5}{2},3]$ | D. | $[\frac{3}{2},5]$ |
6.已知向量$\overrightarrow a=({2,1})$,$\overrightarrow{b}$=(-2,k2),则k=2是$\overrightarrow{a}$⊥$\overrightarrow{b}$的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
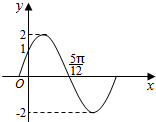 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示,则该函数的解析式为f(x)=2sin(2x+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示,则该函数的解析式为f(x)=2sin(2x+$\frac{π}{6}$).