题目内容
4.已知a、b、c为正数,若a2+b2+4c2=1,求ab+2ac+3$\sqrt{2}$bc的最大值.分析 由a2+b2+4c2=1,可得($\frac{1}{2}+\frac{1}{2}$)a2+($\frac{1}{4}$+$\frac{3}{4}$)b2+(1+3)c2=1,有1=($\frac{1}{2}$a2+$\frac{1}{4}$b2)+($\frac{1}{2}$a2+c2)+($\frac{3}{4}$b2+3c2)$≥2\sqrt{\frac{1}{8}}$ab+2$\sqrt{\frac{1}{2}}$ac+2$\sqrt{\frac{9}{4}}$ac,即可得出结论.
解答 解:∵a2+b2+4c2=1,
∴($\frac{1}{2}+\frac{1}{2}$)a2+($\frac{1}{4}$+$\frac{3}{4}$)b2+(1+3)c2=1,
∴1=($\frac{1}{2}$a2+$\frac{1}{4}$b2)+($\frac{1}{2}$a2+c2)+($\frac{3}{4}$b2+3c2)$≥2\sqrt{\frac{1}{8}}$ab+2$\sqrt{\frac{1}{2}}$ac+2$\sqrt{\frac{9}{4}}$ac
=$\frac{\sqrt{2}}{2}$(ab+2ac+3$\sqrt{2}$bc),
∴ab+2ac+3$\sqrt{2}$bc≤$\sqrt{2}$,
当且仅当a2=$\frac{1}{5}$,b2=$\frac{2}{5}$,c2=$\frac{1}{10}$,ab+2ac+3$\sqrt{2}$bc的最大值是$\sqrt{2}$.
点评 本题考查基本不等式的运用,考查学生的计算能力,正确变形是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.如图,甲、乙两组数据的中位数的和是( )


| A. | 56 | B. | 57 | C. | 58 | D. | 59 |
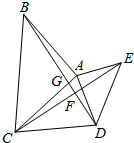 如图,△ABC中,AB=AC,∠BAC=90°,∠ABD=∠ACE,CE=BD,
如图,△ABC中,AB=AC,∠BAC=90°,∠ABD=∠ACE,CE=BD,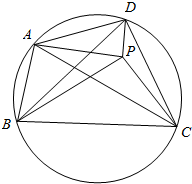 在凸四边形ABCD中,对角线BD不平分对角中的任意一个.点P在四边形ABCD内部,并且满足∠PBC=∠DBA和∠PDC=∠BDA.若A,B,C,D四点共圆,证明:AP=CP.
在凸四边形ABCD中,对角线BD不平分对角中的任意一个.点P在四边形ABCD内部,并且满足∠PBC=∠DBA和∠PDC=∠BDA.若A,B,C,D四点共圆,证明:AP=CP. 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AB⊥AC,AB=AC=1,AA1=2,E、F、G分别是棱BB1、B1C1、CC1的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AB⊥AC,AB=AC=1,AA1=2,E、F、G分别是棱BB1、B1C1、CC1的中点.