题目内容
16.已知极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴,已知曲线C1的极坐标方程ρ=4cosθ,曲线C2的参数方程为$\left\{\begin{array}{l}x=m+tcosα\\ y=tsinα\end{array}\right.(t$为参数,0≤α<π)射线$θ=φ+\frac{π}{4},θ=φ-\frac{π}{4}$与曲线C1交于极点O为的三点A、B、C(1)若|OB|+|OC|=λ|OA|,求λ的值;
(2)当$φ=\frac{π}{12}$时,B、C两点在曲线C2上,求m与α的值.
分析 (1)根据题意表示出|OA|与|OB|,以及|OC|,代入已知等式求出λ的值即可;
(2)根据φ的度数,表示出B与C的极坐标,转化为直角坐标,根据C是经过点(m,0)且倾斜角为α的直线,确定出经过B,C的直线方程,求出m与α的值.
解答 解:(1)根据题意得:|OA|=4cosφ,|OB|=4cos(φ+$\frac{π}{4}$),|OC|=4cos(φ-$\frac{π}{4}$),
则|OB|+|OC|=4cos(φ+$\frac{π}{4}$)+4cos(φ-$\frac{π}{4}$)=2$\sqrt{2}$(cosφ-sinφ)+2$\sqrt{2}$(cosφ+sinφ)=4$\sqrt{2}$cosφ=$\sqrt{2}$|OA|,
∴λ=$\sqrt{2}$;
(2)当φ=$\frac{π}{12}$时,B,C两点的极坐标分别为(2,$\frac{π}{3}$),(2$\sqrt{3}$,-$\frac{π}{6}$)化为直角坐标为B(1,$\sqrt{3}$),C(3,-$\sqrt{3}$),
∵C是经过点(m,0)且倾斜角为α的直线,且经过B,C的直线方程为y=-$\sqrt{3}$(x-2),
∴m=2,α=$\frac{2π}{3}$.
点评 此题考查了参数方程化为普通方程,以及简单曲线的极坐标方程,熟练掌握各坐标之间的转化是解本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
8.已知A(1,3)、B(4,-1)两点,则AB的距离=( )
| A. | 5 | B. | 6 | C. | 7 | D. | 4 |
5.过抛物线y=$\frac{1}{4}$x2的焦点F的直线交抛物线于A,B两点,点O是原点,若|AF|=3,则△AOF的面积为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{47}{32}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
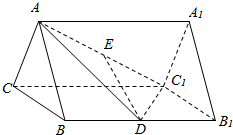 在三棱柱ABC-A1B1C1中,△ABC是边长为2正三角形,D、E分别是线段BB1、AC1的中点,DE⊥AC1.
在三棱柱ABC-A1B1C1中,△ABC是边长为2正三角形,D、E分别是线段BB1、AC1的中点,DE⊥AC1.