题目内容
16.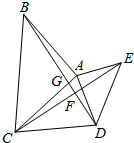 如图,△ABC中,AB=AC,∠BAC=90°,∠ABD=∠ACE,CE=BD,
如图,△ABC中,AB=AC,∠BAC=90°,∠ABD=∠ACE,CE=BD,求证:(1)△ADE也为等腰直角三角形;
(2)BD⊥CE.
分析 (1)由已知条件推导出△ABD≌△ACE,从而得到AD=AE,∠EAC-∠CAD=∠DAB-∠CAD,进而∠EAD=∠CAB=90°,由此能证明△ADE为等腰直角三角形.
(2)由已知∠ABC+∠ACB=180°-∠CAB=90°,∠DBC+∠BCE=90°,由此能证明BD⊥CE.
解答 (1)证明:∵AB=AC,∠ABD=∠ACE,CE=BD,
∴△ABD≌△ACE,
∴AD=AE,∠EAC=∠DAB ,
,
∴∠EAC-∠CAD=∠DAB-∠CAD,
∠EAD=∠CAB=90°,
所以△ADE为等腰直角三角形;
(2)证明:∠ABC+∠ACB=180°-∠CAB=90°,
∠ABD=∠ACE,
(∠ABC-∠ABD)+(∠ACB+∠ACE)=90°,
∠DBC+∠BCE=90°,
∠BFC=180°-(∠DBC+∠BCE)=90°,
∴BD⊥CE.
点评 本题考查三角形是等腰直角三角形的证明,考查两直线垂直的证明,解题时要认真审题,注意三角形全等的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若下列程序执行的结果是100,则输入的x的值是( )


| A. | 0 | B. | 100 | C. | -100 | D. | 100或-100 |
8.已知A(1,3)、B(4,-1)两点,则AB的距离=( )
| A. | 5 | B. | 6 | C. | 7 | D. | 4 |
5.若函数f(x)满足$f(\sqrt{x}+\frac{1}{{\sqrt{x}}})=x+\frac{1}{x}$+1,则函数f(x)的表达式是( )
| A. | x2 | B. | x2+1 | C. | x2-2 | D. | x2-1 |