题目内容
13.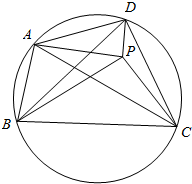 在凸四边形ABCD中,对角线BD不平分对角中的任意一个.点P在四边形ABCD内部,并且满足∠PBC=∠DBA和∠PDC=∠BDA.若A,B,C,D四点共圆,证明:AP=CP.
在凸四边形ABCD中,对角线BD不平分对角中的任意一个.点P在四边形ABCD内部,并且满足∠PBC=∠DBA和∠PDC=∠BDA.若A,B,C,D四点共圆,证明:AP=CP.
分析 设直线DP、BP分别交四边形ABCD的外接圆于E、F两点,由已知条件推导出四边形BEFD、四边形BECA均为等腰梯形,从而得到点P在AC的中垂线上,由此能证明AP=CP.
解答  证明:设直线DP、BP分别交四边形ABCD的外接圆于E、F两点,
证明:设直线DP、BP分别交四边形ABCD的外接圆于E、F两点,
连结EB、EC、EF、FC、FD,
∵∠PBC=∠DBA,∴FC=AD,∴DF∥AC,
∵∠PDC=∠BDA,∴EC=BA,∴BE∥AC,
∴BE∥DF,
∴四边形BEFD、四边形BECA均为等腰梯形,且这两个等腰梯形有共同的对称轴,
∵P是等腰梯形BEFD的对角线的交点,
∴P一定在BE的中垂线上,∴点P在AC的中垂线上,
∴AP=CP.
点评 本题考查线段相等的证明,是中档题,等腰梯形上底的中垂线也是下度的中垂线这个性质,一般很少用作证题的依据,本题中用它证明线段相等新颖、巧妙,不落俗套.

练习册系列答案
相关题目
5.若函数f(x)满足$f(\sqrt{x}+\frac{1}{{\sqrt{x}}})=x+\frac{1}{x}$+1,则函数f(x)的表达式是( )
| A. | x2 | B. | x2+1 | C. | x2-2 | D. | x2-1 |
18.若关于实数x的不等式|x-5|+|x+3|<a无解,则实数a的取值范围是( )
| A. | (-∞,8] | B. | (-∞,8) | C. | (8,+∞) | D. | [8,+∞) |
5.过抛物线y=$\frac{1}{4}$x2的焦点F的直线交抛物线于A,B两点,点O是原点,若|AF|=3,则△AOF的面积为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{47}{32}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
2.已知ab>0,bc<0,则直线ax+by+c=0通过( )
| A. | 第一、二、四象限 | B. | 第一、二、三象限 | C. | 第一、三、四象限 | D. | 第二、三、四象限 |