题目内容
若函数f(x)=
在(-∞,+∞)单调递增,则实数a的取值范围是 .
|
考点:函数单调性的性质
专题:函数的性质及应用
分析:若函数f(x)=
在(-∞,+∞)上单调递增,则每段函数均为增函数,且当x=1时,前一段函数的函数值不大于后一段函数的函数值,由此可构造满足条件的不等式组,解出实数a的取值范围.
|
解答:
解:∵函数f(x)=
在(-∞,+∞)上单调递增,
则
,
解得:a∈[
,2);
故实数a的取值范围是[
,2),
故答案为:[
,2)
|
则
|
解得:a∈[
| 4 |
| 3 |
故实数a的取值范围是[
| 4 |
| 3 |
故答案为:[
| 4 |
| 3 |
点评:本题考查的知识点是函数单调性的性质,熟练掌握分段函数的单调性是解答的关键.

练习册系列答案
相关题目
已知函数f(x)=5x-3sinx,x∈(-2,2),如果f(1-a)+f(1-a2)<0成立,则实数a的取值范围为( )
A、(1,
| ||
| B、(1,3) | ||
| C、(-∞,-2)∪(1,+∞) | ||
| D、(-2,1) |
设定点F1(-3,0),F2(3,0),动点P(x,y)满足条件|PF1|+|PF2|=6,则动点P的轨迹是( )
| A、椭圆 | B、线段 |
| C、双曲线 | D、椭圆或线段 |
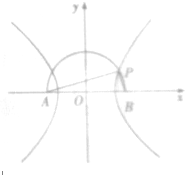 如图,在以点O为圆心,AB为直径的半圆中,P为半圆弧上一点,且AB=4,∠PAB=15°,若A、B分别为双曲线的左、右焦点,则双曲线的标准方程是
如图,在以点O为圆心,AB为直径的半圆中,P为半圆弧上一点,且AB=4,∠PAB=15°,若A、B分别为双曲线的左、右焦点,则双曲线的标准方程是