题目内容
10.在等差数列{an}中,an>0,a7=$\frac{1}{2}$a4+4,Sn为数列{an}的前n项和,S19=152.分析 由等差数列通项公式得a1+9d=a10=4,再由等差数列的前n项和公式得S19=$\frac{19}{2}$(a1+a19)=19a10,由此能求出结果.
解答 解:∵等差数列{an}中,an>0,a7=$\frac{1}{2}$a4+4,
∴${a}_{1}+6d=\frac{1}{2}({a}_{1}+3d)+4$,
解得a1+9d=a10=8,
Sn为数列{an}的前n项和,
则S19=$\frac{19}{2}$(a1+a19)=19a10=152.
故答案为:152.
点评 本题考查了等差数列的通项公式,考查了等差数列的前n项和,是基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
1.执行如图的程序框图,如果输入的x∈[-1,3],输出的y∈[0,4],则输入的a的取值范围为( )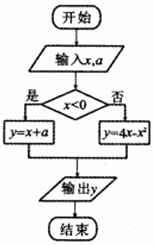

| A. | [-3,4] | B. | [1,4] | C. | [-3,0] | D. | [0,1] |
18.从某高中女学生中选取10名学生,根据其身高(cm)、体重(kg)数据,得到体重关于身高的回归方程$\widehat{y}$=0.85x-85,用来刻画回归效果的相关指数R2=0.6,则下列说法正确的是( )
| A. | 这些女学生的体重和身高具有非线性相关关系 | |
| B. | 这些女学生的体重差异有60%是由身高引起的 | |
| C. | 身高为170cm的学生体重一定为59.5kg | |
| D. | 这些女学生的身高每增加0.85cm,其体重约增加1kg |
15.已知全集U={2,3,4,5,6,7},集合A={4,5,7},B={4,6},则A∩(∁UB)=( )
| A. | {5} | B. | {2} | C. | {2,5} | D. | {5,7} |
17.已知直线(a-2)x+ay-1=0与直线2x+3y-5=0垂直,则a的值为( )
| A. | -6 | B. | 6 | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |