题目内容
18.在半径为1,圆心角为$θ({0<θ≤\frac{π}{2}})$的扇形中,求内接矩形面积的最大值.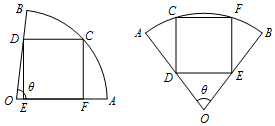
分析 将图二可拆分成两个图一的形式,可以类比得到结论,图一角是θ,图二拆分后角是$\frac{θ}{2}$,故矩形面积的最大值为$\frac{1}{2}tan\frac{θ}{4}$,由此可得结论.
解答 解:图一,设∠COF=x,则CF=rsinx=sinx.
在△OCD中,$\frac{CD}{sin(θ-x)}=\frac{r}{sin(π-θ)}$,
∴CD=$\frac{rsin(θ-x)}{sinθ}$=$\frac{sin(θ-x)}{sinθ}$,
∴矩形面积S=$\frac{sin(θ-x)sinx}{sinθ}$≤$\frac{1-cosθ}{2sinθ}$=$\frac{1}{2}tan\frac{θ}{2}$.
故图一矩形面积的最大值为$\frac{1}{2}tan\frac{θ}{2}$.
图二可拆分成两个,
图一角是θ,图二拆分后角是$\frac{θ}{2}$,故根据图一得出的结论,可得矩形面积的最大值为$\frac{1}{2}tan\frac{θ}{4}$,
而图二时由两个这样的图形组成,
∴两个则为$tan\frac{θ}{4}$.
故图二矩形面积的最大值为$tan\frac{θ}{4}$.
点评 本题考查扇形内接矩形面积问题,考查学生分析解决问题的能力,解题的关键是发现两个图之间的联系,利用已有的结论进行解题,是中档题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目