题目内容
17.如果-1<a<b<0,则下列不等式正确的是( )| A. | $\frac{1}{b}<\frac{1}{a}<{b^2}<{a^2}$ | B. | $\frac{1}{b}<\frac{1}{a}<{a^2}<{b^2}$ | C. | $\frac{1}{a}<\frac{1}{b}<{b^2}<{a^2}$ | D. | $\frac{1}{a}<\frac{1}{b}<{a^2}<{b^2}$ |
分析 根据特殊值法分别带入判断即可.
解答 解:∵-1<a<b<0,
∴不妨令a=-0.5,b=-0.1,
分别带入A、B、C、D,
得:A成立,B、C、D不成立,
故选:A.
点评 本题考查了不等式的性质,考查特殊值法的应用,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.复数z=$\frac{3+2i}{i}$ (i为虚数单位)的虚部为( )
| A. | 3 | B. | -3 | C. | -3i | D. | 2 |
12.直三棱柱A1B1C1-ABC,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,BC=CA=CC1,则BD1与AF1所成角的余弦值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{30}}}{10}$ | C. | $\frac{{\sqrt{30}}}{15}$ | D. | $\frac{{\sqrt{15}}}{10}$ |
9.已知向量$\overrightarrow{a}$=(sinθ,1),$\overrightarrow{b}$=(0,cosθ),θ∈[-$\frac{π}{2}$,$\frac{π}{2}$],则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围是( )
| A. | [0,$\sqrt{2}$] | B. | [0,2] | C. | [1,2] | D. | [$\sqrt{2}$,2] |
6.在三棱锥P-ABC中,PA⊥平面ABC,PA=2$\sqrt{3}$,AC=2,AB=1,∠BAC=60°,则三棱锥P-ABC的外接球的表面积为( )
| A. | 13π | B. | 14π | C. | 15π | D. | 16π |
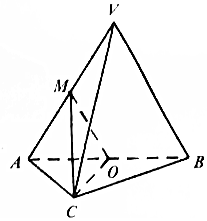 如图,在三棱柱V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.
如图,在三棱柱V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.