题目内容
在平面直角坐标中，△ABC的三个顶点A、B、C，下列结论正确的个数是（ ）
（1）平面内点G满足
+
+
=
，则G是△ABC的重心；
（2）平面内点M满足|
=|
|=|
|，点M是△ABC的内心；
（3）平面内点P满足
=
，则点P在边BC的垂线上．
（1）平面内点G满足
| GA |
| GB |
| GC |
| 0 |
（2）平面内点M满足|
| MA |
| MB |
| MC |
（3）平面内点P满足
| ||||
|
|
| ||||
|
|
| A、0 | B、1 | C、2 | D、3 |
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：结合向量的运算法则和几何意义，推出
=-2
，得G为△ABC的重心说明（1）的正误；
通过距离直接判断（2）正误即可；
通过向量的数量积判断P所在的直线，判断（3）的正误即可．
| GA |
| GD |
通过距离直接判断（2）正误即可；
通过向量的数量积判断P所在的直线，判断（3）的正误即可．
解答：
解：对于（1），取BC的中点D，连接GD，并延长至E，使|DE|=|GD|，则四边形BECG为平行四边形，
∴
+
=
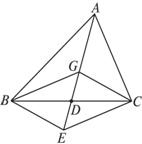=2
．又
+
+
=0，
∴
+
+
=
，即G、A、D三点共线，且G为三等分点，故G为△ABC的重心；（1）正确．
对于（2），平面内点M满足|
=|
|=|
|，点M是△ABC的外心；∴（2）不正确；
对于（3），平面内点P满足
=
，
∴
与
，
方向上的单位向量数量积相等，P在∠APC的平分线上，不一定与BC垂直，∴（3）不正确．
故选：B．
∴| GB |
| GC |
| GE |
| GD |
| GA |
| GB |
| GC |
∴
| GA |
| GB |
| GC |
| 0 |
对于（2），平面内点M满足|
| MA |
| MB |
| MC |
对于（3），平面内点P满足
| ||||
|
|
| ||||
|
|
∴
| AP |
| AB |
| AC |
故选：B．
点评：本题考查向量在几何中的应用，三角形的五心的判断，考查理解判断分析能力．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
角1539°是（ ）
| A、第一象限角 |
| B、第二象限角 |
| C、第三象限角 |
| D、第四象限角 |
将长为L的木棒随机折成3段，则3段构成三角形的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
等差数列{an}中，a1=1，a4=7，则数列{an}的公差为（ ）
| A、1 | B、2 | C、3 | D、4 |
将函数y=sin2x+
cos2x（x∈R）的图象向左平移φ（φ＞0）个单位长度后，所得到的一个偶函数的图象，则φ的最小值是（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|