题目内容
在矩形ABCD中，AB=2AD，M，N分别为AB与CD的中点，则在以A、B、C、D、M、N为起点与终点的所有向量中，相等向量的对数为（ ）
| A、9 | B、11 | C、18 | D、24 |
考点：相等向量与相反向量
专题：平面向量及应用
分析：把所有相等的向量一一列举出来，可得结论．
解答：
解：由题意可得，
=
=
，这里有3对；
=
=
=
，这里有6对；
=
，这里只有1对；
=
，这里有1对，
=
这里有一对，总共12对．
再加上它们的方向相反的12对，总共24对，
故选：D．
| AD |
| MN |
| BC |
| AM |
| MB |
| DN |
| NC |
| AN |
| MC |
| BN |
| MD |
| AB |
| DC |
再加上它们的方向相反的12对，总共24对，
故选：D．
点评：本题主要考查相等的向量和相反的向量，属于基础题．
练习册系列答案
相关题目
直线ax-y+2a=0与曲线y=
相交于相异两点，则实数a的取值范围是（ ）
| 4-(x-1)2 |
A、[-
| ||||||||
B、（-
| ||||||||
C、[0，
| ||||||||
D、[0，
|
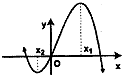已知函数f（x）=ax3+bx2+x（a，b∈R，ab≠0）的图象如图所示（x1，x2为两个极值点），且|x1|＞|x2|则有（ ）| A、a＞0，b＞0 |
| B、a＜0，b＜0 |
| C、a＜0，b＞0 |
| D、a＞0，b＜0 |