题目内容
直线x-4y+6=0和8x+y-18=0与两坐标轴围成的四边形的面积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:直线的一般式方程
专题:直线与圆
分析:求出直线x-4y+6=0和8x+y-18=0交点B的坐标,及直线x-4y+6=0与y轴交点C和直线8x+y-18=0与x轴交点A的坐标,分别计算△OAB和△OBC的面积可得答案.
解答:
解:由
得:
,
故直线x-4y+6=0和8x+y-18=0交点B的坐标为(2,2),
直线x-4y+6=0与y轴交点C的坐标为(0,
),
直线8x+y-18=0与x轴交点A的坐标为(
,0),
故△OAB的面积为:
×2×
=
,
△OBC的面积:
×2×
=
,
故四边形的面积S=
+
=
,
故选:B
|
|
故直线x-4y+6=0和8x+y-18=0交点B的坐标为(2,2),
直线x-4y+6=0与y轴交点C的坐标为(0,
| 3 |
| 2 |
直线8x+y-18=0与x轴交点A的坐标为(
| 9 |
| 4 |
故△OAB的面积为:
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
△OBC的面积:
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
故四边形的面积S=
| 9 |
| 4 |
| 3 |
| 2 |
| 15 |
| 4 |
故选:B
点评:本题考查的知识点是直线的一般式方程,直线的交点,难度不大,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
i是虚数单位,复数
在复平面上的对应点所在直线方程是( )
| 2-i |
| 1+i |
| A、x+y-2=0 |
| B、x-y+2=0 |
| C、x+y+1=0 |
| D、x-y-1=0 |
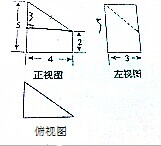 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A、54 | B、60 | C、66 | D、72 |
使
=
成立的α范围( )
|
| cosα-1 |
| sinα |
| A、{x|2kπ-π<α<2kπ,k∈Z} | ||
| B、{x|2kπ-π≤α≤2kπ,k∈Z} | ||
C、{x|2kπ+π<α<2kπ+
| ||
| D、只能是第三或第四象限的角 |