题目内容
4.已知双曲线C1:$\left\{\begin{array}{l}x=3cosα\\ y=2sinα\end{array}$(α为参数),再以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为2ρsinθ+ρcosθ=10.(1)求曲线C1的普通方程和曲线C的直角坐标方程;
(2)若点M在曲线C1上运动,试求出M到曲线C的距离的最小值.
分析 (1)由cos2α+sin2α=1求得曲线C1的普通方程$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1,由y=ρsinθ,x=ρcosθ,曲线C2的直角坐标方程x+2y=10;
(2)使用参数坐标求出点M到曲线C的距离,得到关于θ的三角函数,利用三角函数的性质求出距离的最值.
解答 解:(1)由$\left\{\begin{array}{l}x=3cosα\\ y=2sinα\end{array}$(α为参数),得$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1,
曲线C1的普通方程$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1,
∵y=ρsinθ,x=ρcosθ,
∴曲线C的直角坐标方程x+2y=10;
(2)设M(3cosθ,2sinθ),则距离d=$\frac{|3cosθ+4sinθ-10|}{\sqrt{5}}$≥$\frac{5}{\sqrt{5}}$=$\sqrt{5}$.
点评 本题考查参数方程与普通方程的转化,将极坐标方程转化成直角坐标方程,考查直线与圆的交点问题,属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
6.若无穷等差数列{an}的首项a1<0,公差d>0,{an}的前n项和为Sn,则以下结论中一定正确的是( )
| A. | Sn单调递增 | B. | Sn单调递减 | C. | Sn有最小值 | D. | Sn有最大值 |
12.{an}是各项均为正数的等差数列,{bn}是等比数列,已知$\frac{a_1}{b_1}$=$\frac{a_2}{b_2}$=1,$\frac{a_3}{b_3}$=$\frac{8}{9}$,那么$\frac{a_4}{b_4}$=( )
| A. | $\frac{20}{27}$ | B. | $\frac{16}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{20}{27}$或$\frac{16}{27}$ |
9.设a=log${\;}_{\frac{1}{3}}}$2,b=20.6,c=log43,则a,b,c的大小关系为( )
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | a>c>b |
16.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{5}$,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
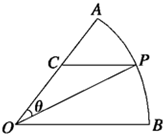 公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形AOB,圆心角AOB的大小等于$\frac{π}{3}$,半径为2百米,在半径OA上取一点C,过点C作平行于OB的直线交弧AB于点P.设∠COP=θ;
公园里有一扇形湖面,管理部门打算在湖中建一三角形观景平台,希望面积与周长都最大.如图所示扇形AOB,圆心角AOB的大小等于$\frac{π}{3}$,半径为2百米,在半径OA上取一点C,过点C作平行于OB的直线交弧AB于点P.设∠COP=θ; 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证: