题目内容
5.“m=-1”是“直线l1:mx+(2m-1)y+1=0与直线l2:3x+my+3=0垂直”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据直线垂直的等价条件求出m的值,结合充分条件和必要条件的定义进行判断即可.
解答 解:若直线l1:mx+(2m-1)y+1=0与直线l2:3x+my+3=0垂直,
则满足3m+m(2m-1)=0,即m(2m+2)=0,
得m=0或m=-1,
则“m=-1”是“直线l1:mx+(2m-1)y+1=0与直线l2:3x+my+3=0垂直”的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,结合直线垂直的等价条件求出m的值是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.设f(x)是定义在R上的函数,它的图象关于点(1,0)对称,当x≤1时,f(x)=2xe-x(e为自然对数的底数),则f(2+3ln2)的值为( )
| A. | 48ln2 | B. | 40ln2 | C. | 32ln2 | D. | 24ln2 |
16.双曲线W:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)一个焦点为F(2,0),若点F到W的渐近线的距离是1,则W的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
13.“=”在基本算法语句中叫( )
| A. | 赋值号 | B. | 等号 | C. | 输入语句 | D. | 输出语句 |
20.直线$x-\sqrt{3}y-1=0$的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
15.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的两个焦点,M(x0,y0)(x0>0,y0>0)是双曲线的渐近线上一点,满足MF1⊥MF2,如果以F2为焦点的抛物线y2=2px(p>0)经过点M,则此双曲线的离心率为( )
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $2+\sqrt{5}$ | D. | $\sqrt{5}-2$ |
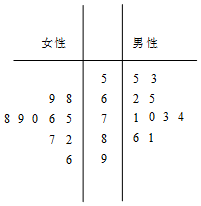 某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:
某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示: