题目内容
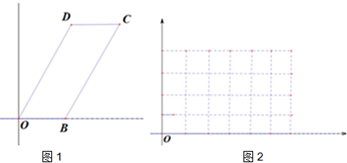
已知OBCD是平行四边形,|OB|=1,|OD|=2,∠BOD=60°,动直线x=t由向右平移,分别交平行四边形两边于不同的两点M,N(如图1).
(1)写出△OMN的面积S关于t的表达式S(t);
(2)画出S(t)的图象(在图2中).
(1)写出△OMN的面积S关于t的表达式S(t);
(2)画出S(t)的图象(在图2中).

考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:本题可以先求出点B、D、C求出直线OD、DC、BC的方程,再根据t的大小,分类讨论,确定点M、N的位置,求出点M、N的坐标,从而得到求出△OMN的面积S关于t的函数;(2)由(1)的结论,分段画出函数S(t)的图象,得到本题结论.
解答:
 解:(1)∵四边形OBCD是平行四边形,|OB|=1,|OD|=2,∠BOD=60°,
解:(1)∵四边形OBCD是平行四边形,|OB|=1,|OD|=2,∠BOD=60°,
∴D(1,
),B(1,0),C(2,
).
∴线段OD的方程为:y=
x,x∈[0,1],
线段BC的方程为:y=
x-
,x∈[1,2],
∵动直线x=t由向右平移,分别交平行四边形两边于不同的两点M,N,
∴当0<t≤1时,直线与OB、OD相交,M(t,
t),N(t,0),
△OMN的面积S关于t的表达式S(t)=
×
t×t=
t2;
当1<t<2时,直线与DC、BC相交,M(t,
),N(t,
t-
),
△OMN的面积S关于t的表达式S(t)=
×t×(
-
t+
)=
(-t2+2t).
∴S(t)=
.
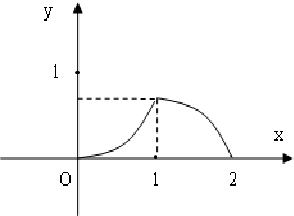
(2)函数S(t)的图象如图:
 解:(1)∵四边形OBCD是平行四边形,|OB|=1,|OD|=2,∠BOD=60°,
解:(1)∵四边形OBCD是平行四边形,|OB|=1,|OD|=2,∠BOD=60°,∴D(1,
| 3 |
| 3 |
∴线段OD的方程为:y=
| 3 |
线段BC的方程为:y=
| 3 |
| 3 |
∵动直线x=t由向右平移,分别交平行四边形两边于不同的两点M,N,
∴当0<t≤1时,直线与OB、OD相交,M(t,
| 3 |
△OMN的面积S关于t的表达式S(t)=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
当1<t<2时,直线与DC、BC相交,M(t,
| 3 |
| 3 |
| 3 |
△OMN的面积S关于t的表达式S(t)=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
∴S(t)=
|
(2)函数S(t)的图象如图:
点评:本题考查了函数的实际应用、还考查了分类讨论的数学思想,本题难度不大,属于基础题.

练习册系列答案
相关题目