题目内容
12.已知$f(x)=\left\{\begin{array}{l}a-{x^2}-2x,x≤0\\{e^{|x-1|}},x>0\end{array}\right.$,且函数y=f(x)-1恰有3个不同的零点,则实数a的取值范围是( )| A. | (-1,+∞) | B. | (-2,0) | C. | (-2,+∞) | D. | (0,1] |
分析 函数的零点的问题也是函数的图象的交点问题,分别画出函数的图象,由图象可知a的范围.
解答 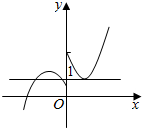 解:∵函数数y=f(x)-1恰有3个不同的零点,
解:∵函数数y=f(x)-1恰有3个不同的零点,
∴f(x)=1有三个解,
即y=f(x)与y=1有三个交点,分别画出函数y=f(x)与y=1的图象,
当x≥0时,f(x)=e|x-1|与y=1只有一个交点,
当x≤0时,f(x)=a-x2-2x=-(x+1)2+a+1.
结合图象可得只需满足:$\left\{\begin{array}{l}a+1>1\\ a≤1\end{array}\right.$,解得0<a≤1,
由图象可知a的范围为(0,1],
故选:D.
点评 本题考查的知识点是根的存在性及根的个数判断,其中熟练掌握函数零点与方程根之间的对应关系是解答的关键

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
3.已知a=($\frac{1}{2}$)${\;}^{\frac{1}{3}}}$,b=($\frac{1}{3}$)${\;}^{-\frac{1}{2}}}$,c=log2$\frac{1}{3}$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
7.某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如下表:
(Ⅰ)求x2的值及函数f(x)的解析式;
(Ⅱ)请说明把函数g(x)=sinx的图象上所有的点经过怎样的变换可以得到函数f(x)的图象.
| x | x1 | $\frac{π}{12}$ | x2 | $\frac{7π}{12}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ)+B | 1 | 4 | 1 | -2 | 1 |
(Ⅱ)请说明把函数g(x)=sinx的图象上所有的点经过怎样的变换可以得到函数f(x)的图象.
17.已知集合A={0,1,2},B={2,3},则集合A∪B=( )
| A. | {1,2,3} | B. | {0,1,2,3} | C. | {2} | D. | {0,1,3} |
2.命题“?x∈R,3x>2x”的否定是( )
| A. | ?x∈R,3x≤2x | B. | ?x∉R,3x<2x | C. | ?x0∈R,3x0≤2x0 | D. | ?x0∉R,3x0<2x0 |
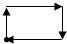
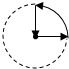
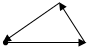
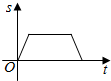 如图是王老师锻炼时所走的离家距离(S)与行走时间(t)之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是( )
如图是王老师锻炼时所走的离家距离(S)与行走时间(t)之间的函数关系图,若用黑点表示王老师家的位置,则王老师行走的路线可能是( )