题目内容
6.当x取何值时,复数z=(x2+x-2)+(x2-3x+2)i(1)是实数?
(2)是纯虚数?
(3)对应的点在第四象限?
分析 (1)z是实数,则虚部等于0,求解即可得答案;
(2)z是纯虚数,则实部等于0,虚部不等于0,求解即可得答案;
(3)由z对应的点在第四象限,列出不等式组,求解即可得答案.
解答 解:(1)复数z=(x2+x-2)+(x2-3x+2)i,
当z是实数时,x2-3x+2=0,解得x=1或x=2;
(2)当z是纯虚数时,$\left\{\begin{array}{l}{x^2}+x-2=0\\{x^2}-3x+2≠0\end{array}\right.$,解得x=-2;
(3)当对应的点在第四象限时,则$\left\{\begin{array}{l}{{x}^{2}+x-2>0}\\{{x}^{2}-3x+2<0}\end{array}\right.$,解得1<x<2,
∴x的取值范围为1<x<2.
点评 本题考查了复数的基本概念,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
17.已知函数f(x)=x3+2x2-3的导函数为f′(x),则f′(-2)等于( )
| A. | 4 | B. | 6 | C. | 10 | D. | 20 |
11.已知数列{an}中,a1=1,an+1=2an+1(n∈N*),则a4的值为( )
| A. | 31 | B. | 30 | C. | 15 | D. | 63 |
18.(x2-$\frac{1}{x}$)6的展开式,x6的系数为( )
| A. | 15 | B. | 6 | C. | -6 | D. | -15 |
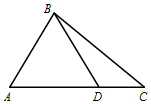 在△ABC中(图),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7},\overrightarrow{AD}=2\overrightarrow{DC}$.
在△ABC中(图),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7},\overrightarrow{AD}=2\overrightarrow{DC}$.