Question

15．已知实数x，y满足不等式组$\left\{\begin{array}{l}y≥x\\ y≤2x\\ x+y≤1\end{array}\right.$，则目标函数z=x+4y的最大值是（　　）

• A． 5
• B． 4
• C． 3
• D． 2

Answer 1

分析 先画出约束条件的可行域，再求出可行域中各角点的坐标，将各点坐标代入目标函数的解析式，分析后易得目标函数Z=x+4y的最大值．

解答 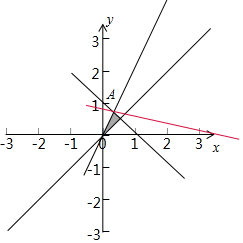解：约束条件$\left\{\begin{array}{l}y≥x\\ y≤2x\\ x+y≤1\end{array}\right.$的可行域如下图示：
由图易得目标函数z=x+4y在A处取得最大值，由$\left\{\begin{array}{l}{x+y=1}\\{y=2x}\end{array}\right.$，解得A（$\frac{1}{3}$，$\frac{2}{3}$），
则目标函数z=x+4y的最大值是：$\frac{1}{3}+\frac{2}{3}×4$=3．
故选：C．

点评 在解决线性规划的小题时，我们常用“角点法”，其步骤为：①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证，求出最优解．