题目内容
设a>0,b>0,a+b=1.
(1)证明:ab+ ≥4
≥4 ;
;
(2)探索猜想,并将结果填在以下括号内:
a2b2+ ≥( );a3b3+
≥( );a3b3+ ≥( );
≥( );
(3)由(1)(2)归纳出更一般的结论,并加以证明.
(1)证明:ab+
 ≥4
≥4 ;
;(2)探索猜想,并将结果填在以下括号内:
a2b2+
 ≥( );a3b3+
≥( );a3b3+ ≥( );
≥( );(3)由(1)(2)归纳出更一般的结论,并加以证明.
证明见解析(2) 16 与64
与64
 与64
与64
(1)证明 方法一 ab+ ≥4
≥4
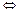 4a2b2-17ab+4≥0
4a2b2-17ab+4≥0
?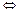 (4ab-1)(ab-4)≥0.
(4ab-1)(ab-4)≥0.
∵ab=( )2≤
)2≤ =
= ,
,
∴4ab≤1,而又知ab≤ <4,
<4,
因此(4ab-1)(ab-4)≥0成立,故ab+ ≥4
≥4 .
.
方法二 ab+ =ab+
=ab+ +
+ ,
,
∵ab≤ =
= ,∴
,∴ ≥4,∴
≥4,∴ ≥
≥ .
.
当且仅当a=b= 时取等号.
时取等号.
又ab+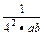 ≥2
≥2 =
= ,
,
当且仅当ab= ,即
,即 =4,a=b=
=4,a=b= 时取等号.
时取等号.
故ab+ ≥
≥ +
+ =4
=4
(当且仅当a=b= 时,等号成立).
时,等号成立).
(2)解 猜想:当a=b= 时,
时,
不等式a2b2+ ≥( )与a3b3+
≥( )与a3b3+ ≥( )取等号,故在括号内分别填16
≥( )取等号,故在括号内分别填16 与64
与64 .
.
(3)解 由此得到更一般性的结论:
anbn+ ≥4n+
≥4n+ .
.
证明如下:
∵ab≤ =
= ,∴
,∴ ≥4.
≥4.
∴anbn+ =anbn+
=anbn+ +
+
≥2 +
+ ×4n
×4n
= +
+ =4n+
=4n+ ,
,
当且仅当ab= ,即a=b=
,即a=b= 时取等号.
时取等号.
 ≥4
≥4
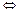 4a2b2-17ab+4≥0
4a2b2-17ab+4≥0?
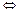 (4ab-1)(ab-4)≥0.
(4ab-1)(ab-4)≥0.∵ab=(
 )2≤
)2≤ =
= ,
,∴4ab≤1,而又知ab≤
 <4,
<4,因此(4ab-1)(ab-4)≥0成立,故ab+
 ≥4
≥4 .
.方法二 ab+
 =ab+
=ab+ +
+ ,
,∵ab≤
 =
= ,∴
,∴ ≥4,∴
≥4,∴ ≥
≥ .
.当且仅当a=b=
 时取等号.
时取等号.又ab+
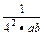 ≥2
≥2 =
= ,
,当且仅当ab=
 ,即
,即 =4,a=b=
=4,a=b= 时取等号.
时取等号.故ab+
 ≥
≥ +
+ =4
=4
(当且仅当a=b=
 时,等号成立).
时,等号成立).(2)解 猜想:当a=b=
 时,
时,不等式a2b2+
 ≥( )与a3b3+
≥( )与a3b3+ ≥( )取等号,故在括号内分别填16
≥( )取等号,故在括号内分别填16 与64
与64 .
.(3)解 由此得到更一般性的结论:
anbn+
 ≥4n+
≥4n+ .
.证明如下:
∵ab≤
 =
= ,∴
,∴ ≥4.
≥4.∴anbn+
 =anbn+
=anbn+ +
+
≥2
 +
+ ×4n
×4n=
 +
+ =4n+
=4n+ ,
,当且仅当ab=
 ,即a=b=
,即a=b= 时取等号.
时取等号.
练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 满足
满足 ,求证
,求证 ≥
≥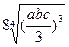
 时,等号成立
时,等号成立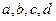 都是实数,求证
都是实数,求证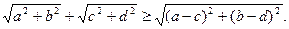
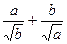 ≥
≥ .
. .
.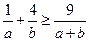 .
.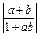 <1.
<1.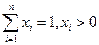 ,求证:
,求证: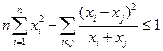 。
。