题目内容
已知|a|<1,|b|<1,求证: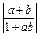 <1.
<1.
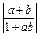 <1.
<1.证明略
∵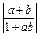 <1
<1
 <1
<1
? a2+b2+2ab<1+2ab+a2b2
a2+b2+2ab<1+2ab+a2b2
? a2b2-a2-b2+1>0
a2b2-a2-b2+1>0
? (a2-1)(b2-1)>0
(a2-1)(b2-1)>0
又|a|<1,|b|<1,∴(a2-1)(b2-1)>0.
∴原不等式成立.
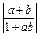 <1
<1
 <1
<1?
 a2+b2+2ab<1+2ab+a2b2
a2+b2+2ab<1+2ab+a2b2?
 a2b2-a2-b2+1>0
a2b2-a2-b2+1>0?
 (a2-1)(b2-1)>0
(a2-1)(b2-1)>0又|a|<1,|b|<1,∴(a2-1)(b2-1)>0.
∴原不等式成立.

练习册系列答案
相关题目
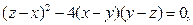 求证:
求证: 成等差数列。
成等差数列。 ≥4
≥4 ;
; ≥( );a3b3+
≥( );a3b3+ ≥( );
≥( );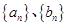 中,
中,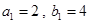 ,且
,且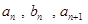 成等差数列,
成等差数列,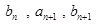 成等比数列
成等比数列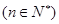 .
.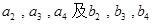 ;
;
 是正实数, 求证:
是正实数, 求证: .
. ≥
≥ .
. z2≥2(xy+yz+zx)
z2≥2(xy+yz+zx) ≥2(
≥2( )
)