题目内容
11.已知向量$\overrightarrow a$,$\overrightarrow b$,其中$|{\overrightarrow a}|=\sqrt{2}$,$|{\overrightarrow b}|=2$,且$({\overrightarrow a-\overrightarrow b})⊥\overrightarrow a$,则$|{2\overrightarrow a-\overrightarrow b}|$=2.分析 利用向量垂直的条件,结合向量数量积公式,即可求向量$\overrightarrow{a}$和$\overrightarrow{b}$的夹角,从而求出$|{2\overrightarrow a-\overrightarrow b}|$的值.
解答 解:设向量$\overrightarrow{b}$和$\overrightarrow{a}$的夹角是α,则
∵|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$,
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=2-$\overrightarrow{a}$•$\overrightarrow{b}$=2-2$\sqrt{2}$cosα
∴cosα=$\frac{\sqrt{2}}{2}$,
∴${(|2\overrightarrow{a}-\overrightarrow{b}|)}^{2}$=4${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$-4$\overrightarrow{a}$•$\overrightarrow{b}$=8+4-4×$\sqrt{2}$×2×$\frac{\sqrt{2}}{2}$=4
故$|{2\overrightarrow a-\overrightarrow b}|$=2,
故答案为:2.
点评 本题考查向量的夹角的计算,考查向量数量积公式的运用,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
20.今有点A(-4,3)在双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)上,过点A的直线l与双曲线相切,且与双曲线两渐近线围成的三角形面积为2$\sqrt{3}$,则直线l的方程为( )
| A. | x+y+1=0 | B. | 2x+y+5=0 | C. | 2x+3y+1=0 | D. | x+3y-5=0 |
16.已知集合A={x|-2<x<1},B={x|x>0},则集合A∪B等于( )
| A. | {x|x>-2} | B. | {x|0<x<1} | C. | {x|x<1} | D. | {x|-2<x<1} |
2.△ABC中,角A,B,C对应的边分别为a,b,c,若sinA,sinB,sinC成等差数列,且$tanC=2\sqrt{2}$,则$\frac{sinB}{sinA}$等于( )
| A. | $\frac{10}{9}$ | B. | $\frac{14}{9}$ | C. | $\frac{5}{3}$ | D. | $\frac{3}{2}$ |
18.若函数$f(x)={log_{\frac{1}{3}}}x+\frac{1}{x}+a$的零点在区间(1,+∞)上,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (-∞,-1) | C. | (-1,+∞) | D. | (0,+∞) |
19.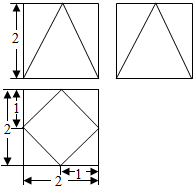 一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )
一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )
 一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )
一个正方体截去四个角得到一个多面体,其三视图如图所示,则该多面体的体积为( )| A. | 4 | B. | $\frac{20}{3}$ | C. | $\frac{4}{3}$(3+$\sqrt{2}$) | D. | $\frac{16}{3}$ |
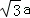 =2csinA
=2csinA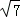 ,且△ABC的面积为
,且△ABC的面积为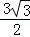 ,求a+b的值
,求a+b的值