题目内容
4.大学生甲、乙两人独立地参加论文答辩,他们的导师根据他们的论文质量估计他们都能过关的概率为$\frac{1}{2}$,甲过而乙没过的概率为$\frac{1}{4}$(导师不参与自己学生的论文答辩),则导师估计乙能过关的概率为$\frac{2}{3}$.分析 设导师估计甲、乙能过关的概率分别为p,q,由已知列出方程组,能求出导师估计乙能过关的概率.
解答 解:设导师估计甲、乙能过关的概率分别为p,q,
则$\left\{\begin{array}{l}{pq=\frac{1}{2}}\\{p(1-q)=\frac{1}{4}}\end{array}\right.$,
解得p=$\frac{3}{4}$,q=$\frac{2}{3}$.
∴导师估计乙能过关的概率为$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意互斥事件概率加法公式和相互独立事件概率乘法公式的合理运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
9.复数$\frac{1-{i}^{3}}{1+3i}$=( )
| A. | -$\frac{2}{5}$+$\frac{1}{5}$i | B. | -$\frac{2}{5}$-$\frac{1}{5}$i | C. | $\frac{2}{5}$+$\frac{1}{5}$i | D. | $\frac{2}{5}$-$\frac{1}{5}$i |
10.近日,济南楼市迎来去库存一系列新政,其中房产税收中的契税和营业税双双下调,对住房市场持续增长和去库存产生积极影响.某房地产公司从两种户型中各拿出9套进行促销活动,其中A户型每套面积100平方米,均价1.1万元/平方米,B户型每套面积80平方米,均价1.2万元/平方米.下表是这18套住宅平方米的销售价格:(单位:万元/平方米):
(I)求a,b的值;
(II)张先生想为自己和父母买两套售价小于100万元的房子,求至少有一套面积为100平方米的概率.
| 房号/户型 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A户型 | 0.98 | 0.99 | 1.06 | 1.17 | 1.10 | 1.21 | a | 1.09 | 1.14 |
| B户型 | 1.08 | 1.11 | 1.12 | b | 1.26 | 1.27 | 1.26 | 1.25 | 1.28 |
(II)张先生想为自己和父母买两套售价小于100万元的房子,求至少有一套面积为100平方米的概率.
 中,
中, ,
, ,则
,则 ( )
( )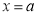 与函数
与函数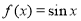 和
和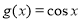 的图像分别交于
的图像分别交于 两点,则
两点,则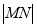 的最大值为( )
的最大值为( )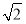 C.
C.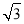 D.2
D.2