题目内容
2.△ABC中,角A,B,C对应的边分别为a,b,c,若sinA,sinB,sinC成等差数列,且$tanC=2\sqrt{2}$,则$\frac{sinB}{sinA}$等于( )| A. | $\frac{10}{9}$ | B. | $\frac{14}{9}$ | C. | $\frac{5}{3}$ | D. | $\frac{3}{2}$ |
分析 由题意可得c=2b-a,cosC=$\frac{1}{3}$,代入余弦定理可得$\frac{b}{a}$=$\frac{10}{9}$,再由正弦定理可得.
解答 解:∵△ABC中sinA,sinB,sinC成等差数列,
∴2sinB=sinA+sinC,由正弦定理2b=a+c,即c=2b-a,
∵$tanC=2\sqrt{2}$,∴由同角三角函数基本关系可得cosC=$\frac{1}{3}$,
∴由余弦定理可得c2=a2+b2-2abcosC=a2+b2-$\frac{2}{3}$ab,
故(2b-a)2=a2+b2-$\frac{2}{3}$ab,整理可得3b2=$\frac{10}{3}$ab,
解得$\frac{b}{a}$=$\frac{10}{9}$,由正弦定理可得$\frac{sinB}{sinA}$=$\frac{b}{a}$=$\frac{10}{9}$,
故选:A.
点评 本题考查正弦定理解三角形,涉及等差数列和同角三角函数基本关系,属中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
10.近日,济南楼市迎来去库存一系列新政,其中房产税收中的契税和营业税双双下调,对住房市场持续增长和去库存产生积极影响.某房地产公司从两种户型中各拿出9套进行促销活动,其中A户型每套面积100平方米,均价1.1万元/平方米,B户型每套面积80平方米,均价1.2万元/平方米.下表是这18套住宅平方米的销售价格:(单位:万元/平方米):
(I)求a,b的值;
(II)张先生想为自己和父母买两套售价小于100万元的房子,求至少有一套面积为100平方米的概率.
| 房号/户型 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A户型 | 0.98 | 0.99 | 1.06 | 1.17 | 1.10 | 1.21 | a | 1.09 | 1.14 |
| B户型 | 1.08 | 1.11 | 1.12 | b | 1.26 | 1.27 | 1.26 | 1.25 | 1.28 |
(II)张先生想为自己和父母买两套售价小于100万元的房子,求至少有一套面积为100平方米的概率.
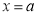 与函数
与函数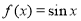 和
和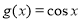 的图像分别交于
的图像分别交于 两点,则
两点,则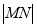 的最大值为( )
的最大值为( )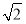 C.
C.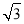 D.2
D.2