题目内容
17.某四棱锥的三视图如图所示,则该四棱锥的表面积为( )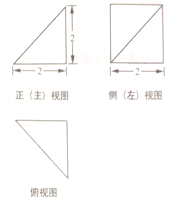
| A. | $8+4\sqrt{2}$ | B. | $6+\sqrt{2}+2\sqrt{3}$ | C. | $6+4\sqrt{2}$ | D. | $6+2\sqrt{2}+2\sqrt{3}$ |
分析 由已知中的三视图,可知该几何体是一个正方形为底面的四棱锥,把该三视图还原成直观图,累加各个面的面积可得,几何体的表面积.
解答 解:该三视图还原成直观图后的几何体是如图的四棱锥,红色线四棱锥A-BCDE为三视图还原后的几何体,
CBA和ACD是两个全等的直角三角形:AC=CD=BC=2
∴两个全等的直角三角形面积为:4.
底面DCBE是正方形,边长为2,
∴底面的正方形面积为:4.
ABE是直角三角形,AB=$2\sqrt{2}$,BE=2,
∴面积为:$2\sqrt{2}$.
AED是直角三角形,DE=2,AD=$2\sqrt{2}$,
∴面积为:$2\sqrt{2}$.
该四棱锥的表面积为4+4+2$\sqrt{2}$+2$\sqrt{2}$=$8+4\sqrt{2}$.
故选:A.
点评 本题考查的知识点是由三视图求表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
8.函数f(x)=$\frac{2}{{{x^2}+2}}$(x∈R)的值域是( )
| A. | (0,1) | B. | (0,1] | C. | [0,1) | D. | [0,1] |
5.下列几何图形中,可能不是平面图形的是( )
| A. | 梯形 | B. | 菱形 | C. | 平行四边形 | D. | 四边形 |
7.若角α的顶点为坐标原点,始边在x轴的非负半轴上,终边在直线$y=-\sqrt{3}x$上,则角α的取值集合是( )
| A. | $\{α|α=2kπ-\frac{π}{3},k∈Z\}$ | B. | $\{α|α=2kπ+\frac{2π}{3},k∈Z\}$ | C. | $\{α|α=kπ-\frac{2π}{3},k∈Z\}$ | D. | $\{α|α=kπ-\frac{π}{3},k∈Z\}$ |
 如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.
如图,已知斜三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,且BA1⊥AC1.