题目内容
9.设函数f(x)=|2x+3|+|x-1|.(1)解不等式f(x)>4;
(2)若存在x0∈[-$\frac{3}{2}$,1],使不等式a+1>f(x0) 成立,求实数a的取值范围.
分析 (1)先求出f(x)的表达式,得到关于x的不等式组,解出即可;
(2)问题转化为:a+1>(f(x))min,求出f(x)的最小值,从而求出a的范围即可.
解答 解:(1)∵f(x)=|2x+3|+|x-1|,
∴f(x)=$\left\{\begin{array}{l}{-3x-2,x<-\frac{3}{2}}\\{x+4,-\frac{3}{2}≤x≤1}\\{3x+2,x>1}\end{array}\right.$,
∴f(x)>4?$\left\{\begin{array}{l}{x<-\frac{3}{2}}\\{-3x-2>4}\end{array}\right.$ 或$\left\{\begin{array}{l}{-\frac{3}{2}≤x≤1}\\{x+4>4}\end{array}\right.$ 或$\left\{\begin{array}{l}{x>1}\\{3x+2>4}\end{array}\right.$,
?x<-2或0<x≤1或x>1,
综上所述,不等式的解集为:(-∞,-2)∪(0,+∞);
(2)若存在x∈[-$\frac{3}{2}$,1]使不等式a+1>f(x)成立,
?a+1>(f(x))min,
由(1)知,x∈[-$\frac{3}{2}$,1]时,f(x)=x+4,
∴x=-$\frac{3}{2}$时,(f(x))min=$\frac{5}{2}$,
a+1>$\frac{5}{2}$?a>$\frac{3}{2}$,
∴实数a的取值范围为($\frac{3}{2}$,+∞).
点评 本题考察了绝对值不等式的解法,考察转化思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知命题p:?x>0,都有(x+1)ex>1.则¬p为( )
| A. | ?x≤0,总有(x+1)ex≤1 | B. | ?x0>0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | ||
| C. | ?x0≤0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | D. | ?x>0,总有(x+1)ex≤1 |
20.已知$a_1^2+b_1^2≠0$,$a_2^2+b_2^2≠0$,则“$|{\begin{array}{l}{a_1}&{b_1}\\{{a_2}}&{b_2}\end{array}}|≠0$”是“直线a1x+b1y+c1=0与直线a2x+b2y+c2=0”平行的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
17.某四棱锥的三视图如图所示,则该四棱锥的表面积为( )
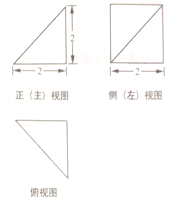

| A. | $8+4\sqrt{2}$ | B. | $6+\sqrt{2}+2\sqrt{3}$ | C. | $6+4\sqrt{2}$ | D. | $6+2\sqrt{2}+2\sqrt{3}$ |