题目内容
19.已知向量|$\overrightarrow{a}$|=1,$\overrightarrow{a}•\overrightarrow{b}$=1,则|$\overrightarrow{b}$|min=1.分析 运用向量数量积的定义和余弦函数的值域,结合条件,即可得到所求最小值.
解答 解:向量|$\overrightarrow{a}$|=1,$\overrightarrow{a}•\overrightarrow{b}$=1,
可得|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=1,
由|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>|≤1,
可得$\frac{1}{|\overrightarrow{b}|}$=cos<$\overrightarrow{a}$,$\overrightarrow{b}$>≤1,
可得|$\overrightarrow{b}$|≥1,
当$\overrightarrow{a}$,$\overrightarrow{b}$同向时,取得最小值1.
故答案为:1.
点评 本题考查向量模的最小值的求法,注意运用向量数量积的定义和余弦函数的值域,考查运算能力,属于基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
9.已知双曲线的中心在原点O,左焦点为F1,圆O过点F1,且与双曲线的一个交点为P,若直线PF1的斜率为$\frac{1}{3}$,则双曲线的渐近线方程为( )
| A. | y=±x | B. | y=±$\frac{\sqrt{6}}{3}$x | C. | y=±$\frac{\sqrt{6}}{4}$x | D. | y=±$\frac{\sqrt{6}}{2}$x |
14.“Z=$\frac{1}{sinθ+cosθ•i}$-$\frac{1}{2}$(其中i是虚数单位)是纯虚数.”是“θ=$\frac{π}{6}$+2kπ”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
11.已知非零向量$\overrightarrow m$,$\overrightarrow n$满足|$\overrightarrow m|=2|\overrightarrow n|$,cos<$\overrightarrow m,\overrightarrow n>=\frac{1}{3}$,若$\overrightarrow m⊥(t\overrightarrow n+\overrightarrow m)$,则实数t的值为( )
| A. | -6 | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
8.已知直线a⊥平面α,则“直线b∥平面α”是“直线a⊥直线b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\overrightarrow{SF}=λ\overrightarrow{SC}$,SA∥平面BEF.
已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\overrightarrow{SF}=λ\overrightarrow{SC}$,SA∥平面BEF.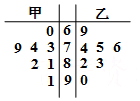 某人到甲、乙两市各7个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )
某人到甲、乙两市各7个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( ) 在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.
在四棱锥P-ABCD中,AD∥BC,AD=AB=DC=$\frac{1}{2}$BC=1,E是PC的中点,面PAC⊥面ABCD.