题目内容
已知在△ABC中，A，B，C为其内角，若2sinA•cosB=sinC，判断三角形的形状．
考点：三角形的形状判断
专题：解三角形
分析：依题意，利用诱导公式及两角和与差的正弦可求得sin（A-B）=0，从而可判断三角形的形状．
解答：
解：在△ABC中，∵2sinA•cosB=sinC=sin[π-（A+B）]=sin（A+B）=sinA•cosB+cosAsinB，
∴sinA•cosB-cosAsinB=sin（A-B）=0，
∴A-B=0，
∴A=B．
故△ABC为等腰三角形．
∴sinA•cosB-cosAsinB=sin（A-B）=0，
∴A-B=0，
∴A=B．
故△ABC为等腰三角形．
点评：本题考查三角形的形状的判断，考查两角和与差的正弦，属于中档题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
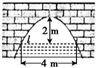2013年国家加大了对环境污染监测力度，为此某市环保部门在市里的一条污水河的桥孔处进行了隔离封闭改造，桥孔的横断面为抛物线形（如下图所示），已知水面在l时，拱顶离水面2米，水面宽4米，则水上升0.5米后，水面宽变为函数y=
+1（x≥2）的反函数是（ ）
| x-2 |
| A、y=2-（x-1）2（x≥2） |
| B、y=2+（x-1）2（x≥2） |
| C、y=2-（x-1）2（x≥1） |
| D、y=2+（x-1）2（x≥1） |