题目内容
9.函数f(x)=3sinx-log2x的零点个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 令y=3sinx,y=log2x,作两个函数的图象求交点个数即可.
解答 解:令y=3sinx,y=log2x,
作两个函数的图象如下,
结合图象可知,
两个函数的图象有三个不同的交点,
故函数f(x)=3sinx-log2x的零点个数是3;
故选:C.
点评 本题考查了函数的零点与函数的交点的关系应用,同时考查了数形结合的思想应用.

练习册系列答案
相关题目
19.设直线l的方向向量是$\overrightarrow{u}$=(-2,2,t),平面α的法向量$\overrightarrow{v}$=(6,-6,12),若直线l⊥平面α,则实数t等于( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
20.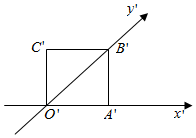 如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )
如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )
 如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )
如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )| A. | 2$\sqrt{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | 2(1+$\sqrt{3}$) | D. | 6 |
17.已知函数f(x)=xn的图象过点(3,$\sqrt{3}$),则n=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
18.下列函数在定义域上不是连续函数的是( )
| A. | f(x)=x2 | B. | f(x)=x | C. | f(x)=$\sqrt{x}$ | D. | f(x)=$\frac{1}{x}$ |
19.已知正四面体ABCD,点E,F分别为棱AB,AC的中点,球O是正四面体ABCD的外接球,球O截直线EF所得的弦长为6$\sqrt{5}$,则正四面体的棱长为( )
| A. | 6$\sqrt{5}$ | B. | 12 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{2}$ |
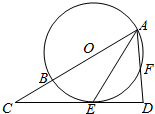 如图所示,⊙O的圆心O在Rt△ACD的斜边AC上,且⊙O过顶点A,与边CD相切于点E,与边AD、AC分别相交于点F,B.
如图所示,⊙O的圆心O在Rt△ACD的斜边AC上,且⊙O过顶点A,与边CD相切于点E,与边AD、AC分别相交于点F,B.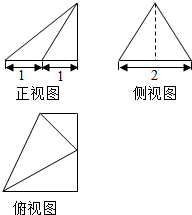 某几何体的三视图(单位:cm)如图所示,其中侧视图是一个边长为2的正三角形,则这个几何体的体积为$\sqrt{3}$.
某几何体的三视图(单位:cm)如图所示,其中侧视图是一个边长为2的正三角形,则这个几何体的体积为$\sqrt{3}$.