题目内容
11.若函数f(x)=$\left\{\begin{array}{l}-({x+1})•{e^x},x≤a\\-2x-1,x>a\end{array}$有最大值,则实数a的取值范围是( )| A. | $[{-\frac{1}{2}-\frac{1}{{2{e^2}}},+∞})$ | B. | $[{-\frac{1}{{2{e^2}}},+∞})$ | C. | [-2,+∞) | D. | $({-2,-\frac{1}{2}-\frac{1}{{2{e^2}}}}]$ |
分析 由x>a时,f(x)=-2x-1递减,且无最大值,可得x≤a时,f(x)取得最大值M,且M≥-2a-1,求出x≤a时,f(x)的导数和单调区间、极大值,讨论a<-2,判断单调性,可得最大值,解不等式判断无解,则a≥-2,求出最大值,解不等式即可得到所求a的范围.
解答 解:由x>a时,f(x)=-2x-1递减,可得f(x)<-2a-1,无最大值,
函数f(x)=$\left\{\begin{array}{l}-({x+1})•{e^x},x≤a\\-2x-1,x>a\end{array}$有最大值,
可得x≤a时,f(x)取得最大值M,且M≥-2a-1,
由f(x)=-(x+1)•ex的导数为f′(x)=-(x+2)ex,
可得x>-2时,f′(x)<0,f(x)递减;x<-2时,f′(x)>0,f(x)递增.
即有f(x)在x=-2处取得极大值,且为最大值e-2.
若a<-2,则f(x)在(-∞,a]递增,可得f(x)≤f(a)=-(a+1)•ea,
由题意可得-(a+1)•ea≥-2a-1,
即有(a+1)•ea-2a-1≤0,
由g(a)=(a+1)•ea-2a-1的导数为g′(a)=(a+2)•ea-2<0,(a<-2),
则g(a)在a<-2递减,可得g(a)>g(-2)=-e-2+3>0,
则不等式(a+1)•ea-2a-1≤0无实数解.
故a≥-2,可得x=-2处f(x)取得最大值,且为-e-2,
由-e-2≥-2a-1,
解得a≥-$\frac{1}{2}$-$\frac{1}{2{e}^{2}}$,
综上可得,a的范围是[-$\frac{1}{2}$-$\frac{1}{2{e}^{2}}$,+∞).
故选:A.
点评 本题考查分段函数的最值问题,考查转化思想,以及分类讨论思想方法,注意运用导数,求出单调区间和极值、最值,考查化简整理的运算能力,属于中档题.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案| A. | [-1,2) | B. | [-1,2] | C. | [-4,1] | D. | [-1,4] |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\sqrt{3}$ | B. | 3 | C. | 2 | D. | $2\sqrt{3}$ |
| A. | $({\sqrt{2},+∞})$ | B. | $[{\sqrt{2},+∞})$ | C. | $({1,\sqrt{2}})$ | D. | $({1,\sqrt{2}}]$ |
| A. | -112 | B. | -56 | C. | 112 | D. | 56 |
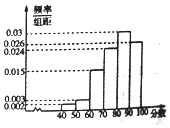 2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图:
2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图: